
【题目】如图所示,已知一次函数![]() 的图象与
的图象与![]() 轴,
轴,![]() 轴分别交于点
轴分别交于点![]() 、
、![]() .以
.以![]() 为边在第一象限内作等腰
为边在第一象限内作等腰![]() ,且
,且![]() ,
,![]() .过
.过![]() 作
作![]() 轴于
轴于![]() .
.![]() 的垂直平分线
的垂直平分线![]() 交
交![]() 与点
与点![]() ,交
,交![]() 轴于点
轴于点![]() .
.
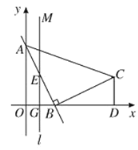
(1)求点![]() 的坐标;
的坐标;
(2)在直线![]() 上有点
上有点![]() ,且点
,且点![]() 与点
与点![]() 位于直线
位于直线![]() 的同侧,使得
的同侧,使得![]() ,求点
,求点![]() 的坐标.
的坐标.
(3)在(2)的条件下,连接![]() ,判断
,判断![]() 的形状,并给予证明.
的形状,并给予证明.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)等腰直角三角形,证明见详解.
;(3)等腰直角三角形,证明见详解.
【解析】
(1)证![]() ,
,![]() ,
,![]() .
.
(2)由![]() 可知作
可知作![]() 的一半的面积与
的一半的面积与![]() 相等,可作一条过AC的中点的平行于AB的直线将会交
相等,可作一条过AC的中点的平行于AB的直线将会交![]() 于M点,证
于M点,证![]() ,
, ![]() ,
,![]() .
.
(3)E、G分别为![]() 的中点,知
的中点,知![]() ,
,![]() ,
,![]() ,
,![]() 为矩形,
为矩形,![]() ,
,![]() ,
,![]() ,可判断
,可判断![]() ,即可得
,即可得![]() 的形状.
的形状.
(1)∵![]() 的图象与
的图象与![]() 轴、
轴、![]() 轴分别交于点
轴分别交于点![]() 、
、![]() ,
,
∴可得![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
在![]() 与
与![]() 中,
中,
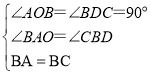 ,
,
∴![]() ;
;
∴![]() ,
,![]() ;
;
∴![]() ;
;
∴![]()
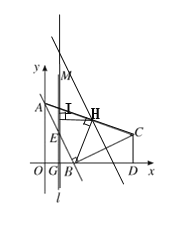
(2)如下图作一条过AC的中点H点的平行于AB的直线将会交![]() 于一点,由A、C点可得H点坐标
于一点,由A、C点可得H点坐标![]() ,
,
∵![]() ,
,![]()
∴![]() ,
,
∴![]() 与
与![]() 的高相等,即过H点的平行于AB的直线将会交
的高相等,即过H点的平行于AB的直线将会交![]() 于M点
于M点
∵![]() ,
,
∴![]()
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
如下图过H点作![]() 的垂线交于I点,
的垂线交于I点,![]() ,得
,得![]() ,
,![]() ,
,
在![]() 与
与![]() 中,
中,
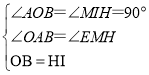 ,
,
∴![]() ;
;
∴![]() ,
,
∴![]() ;
;
∴![]()
(3)∵E、G分别为![]() 的中点,
的中点,
∴![]() ,
,
∵![]() ,
,![]()
∴![]() 为矩形;
为矩形;
∴![]() ,
,![]() ,
,![]()
∵![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,得
,得![]() ,
,
∴![]() 为等腰直角三角形;
为等腰直角三角形;


科目:初中数学 来源: 题型:
【题目】(10分)已知E,F分别为正方形ABCD的边BC,CD上的点,AF,DE相交于点G,当E,F分别为边BC,CD的中点时,有:①AF=DE;②AF⊥DE成立.
试探究下列问题:
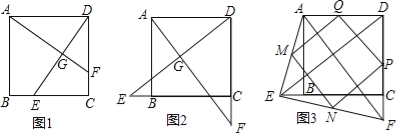
(1)如图1,若点E不是边BC的中点,F不是边CD的中点,且CE=DF,上述结论①,②是否仍然成立?(请直接回答“成立”或“不成立”),不需要证明)
(2)如图2,若点E,F分别在CB的延长线和DC的延长线上,且CE=DF,此时,上述结论①,②是否仍然成立?若成立,请写出证明过程,若不成立,请说明理由;
(3)如图3,在(2)的基础上,连接AE和BF,若点M,N,P,Q分别为AE,EF,FD,AD的中点,请判断四边形MNPQ是“矩形、菱形、正方形”中的哪一种,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某天猫店销售某种规格学生软式排球,成本为每个30元.以往销售大数据分析表明:当每只售价为40元时,平均每月售出600个;若售价每上涨1元,其月销售量就减少20个,若售价每下降1元,其月销售量就增加200个.
(1)若售价上涨m元,每月能售出 个排球(用m的代数式表示).
(2)为迎接“双十一”,该天猫店在10月底备货1300个该规格的排球,并决定整个11月份进行降价促销,问售价定为多少元时,能使11月份这种规格排球获利恰好为8400元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在杭州西湖风景游船处,如图,在离水面高度为5m的岸上,有人用绳子拉船靠岸,开始时绳子BC的长为13m,此人以0.5m/s的速度收绳.10s后船移动到点D的位置,问船向岸边移动了多少m?(假设绳子是直的,结果保留根号)
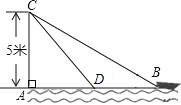
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC与△AEF中,AB=AE,BC=EF,∠B=∠E,AB交EF于D.给出下列结论:①AF=AC;②DF=CF;③∠AFC=∠C;④∠BFD=∠CAF.
其中正确的结论个数有. ( )
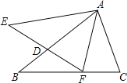
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
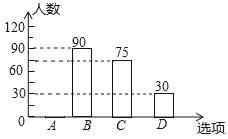
【题目】某校决定在4月7日开展“世界无烟日”宣传活动,活动有A社区板报、B集会演讲、C喇叭广播、D发宣传画四种宣传方式.学校围绕“你最喜欢的宣传方式是什么?”,在全校学生中进行随机抽样调查四个选项中必选且只选一项,根据调查统计结果,绘制了两种不完整的统计图表.
选项 | 方式 | 百分比 |
A | 社区板报 | m |
B | 集会演讲 | 30% |
C | 喇叭广播 | 25% |
D | 发宣传画 | 10% |
请结合统计图表,回答下列问题:
(1)本次抽查的学生共 人,m= ,并将条形统计图补充完整;
(2)若该校学生有900人,请你估计该校喜欢“集会演讲”这项宣传方式的学生约有多少人?
(3)学校采用抽签方式让每班在A、B、C、D四种宣传方式中随机抽取两种进行展示.请用树状图或列表法求某班所抽到的两种方式恰好是“集会演讲”和“喇叭广播”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明想了解全校3000名同学对新闻、体育、音乐、娱乐、戏曲五类电视节目的喜爱况,从中抽取了一部分同学进行了一次抽样调查,利用所得数据绘制成下面的统计图:根据图中所给信息,全校喜欢娱乐类节目的学生大约有( )人.
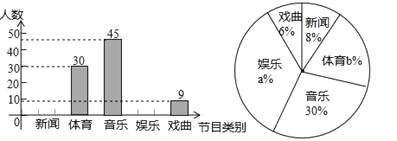
A. 1080 B. 900 C. 600 D. 108
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一面靠墙(墙的最大可用长度为8 m)的空地上用长为24 m的篱笆围成中间隔有二道篱笆的长方形花圃.设花圃的宽AB为x m,面积为S m2.
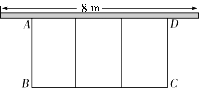
(1)求S关于x的函数关系式及自变量的取值范围;
(2)求所围成花圃的最大面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com