
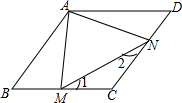
 在菱形ABCD中,M,N分别是边BC,CD上的点,且AM=AN=MN=AB,则∠C的度数为( )
在菱形ABCD中,M,N分别是边BC,CD上的点,且AM=AN=MN=AB,则∠C的度数为( )| A. | 120° | B. | 100° | C. | 80° | D. | 60° |
分析 由菱形的性质和已知条件得出:AB=AM,AN=AD,△AMN是等边三角形,得出∠B=∠AMB,∠D=∠AND,∠MAN=60°,设∠B=x,则∠AMB=x,∠BAM=∠DAN=180°-2x,根据题意列出方程,解方程即可得出结果.
解答 解:∵四边形ABCD是菱形,
∴AB=AD,
∵AM=AN=MN=AB,
∴AB=AM,AN=AD,△AMN是等边三角形,
∴∠B=∠AMB,∠D=∠AND,∠MAN=60°,
设∠B=x,则∠AMB=x,∠BAM=∠DAN=180°-2x,
∵∠B+∠BAD=180°,
∴x+180°-2x+60°+180°-2x=180°,
解得:x=80°,
∴∠B=80°,
∴∠C=180°-80°=100°;
故选:B.
点评 本题考查了菱形的性质、等腰三角形的性质以及等边三角形的性质;由角之间的数量关系设出未知数列出方程是解决问题的关键.


 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 448×108 | B. | 44.8×109 | C. | 4.48×1010 | D. | 4×1010 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x≠1 | B. | x>-3且x≠1 | C. | x≥-3 | D. | x≥-3且x≠1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2 015 | B. | -2 015 | C. | $\frac{1}{2015}$ | D. | -$\frac{1}{2015}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com