
【题目】如图所示,小明在自家楼顶上的点A处测量建在与小明家楼房同一水平线上邻居的电梯的高度,测得电梯楼顶部B处的仰角为45°,底部C处的俯角为26°,已知小明家楼房的高度AD=15米,求电梯楼的高度BC(结果精确到0.1米)(参考数据:sin26°≈0.44,cos26°≈0.90,tan26°≈0.49)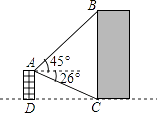
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC的内切圆⊙O与两直角边AB,BC分别相切于点D,E,过劣弧 ![]() (不包括端点D,E)上任一点P作⊙O的切线MN与AB,BC分别交于点M,N,若⊙O的半径为r,则Rt△MBN的周长为( )
(不包括端点D,E)上任一点P作⊙O的切线MN与AB,BC分别交于点M,N,若⊙O的半径为r,则Rt△MBN的周长为( ) 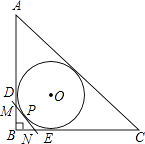
A.r
B.![]() ?r
?r
C.2r
D.![]() ?r
?r
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A、B、C、D、E在同一直线上,且AC=BD,E是线段BC的中点.
![]()
(1)点E是线段AD的中点吗?说明理由;
(2)当AD=10,AB=3时,求线段BE的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,点E、F分别是BC、CD上的点,且CE=CF,点P、Q分别是AF、EF的中点,连接PD、PQ、DQ,则△PQD的形状是( )
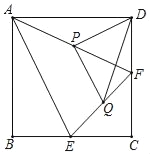
A. 等腰三角形 B. 直角三角形
C. 等腰非直角三角形 D. 等腰直角三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在△ABC中,AC=a,AB与BC所在直线成45°角,AC与BC所在直线形成的夹角的余弦值为 ![]() (即cosC=
(即cosC= ![]() ),则AC边上的中线长是 .
),则AC边上的中线长是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某广告公司招标了一批灯箱加工工程,需要在规定时间内加工1400个灯箱,该公司按一定速度加工5天后,发现按此速度加工下去会延期10天完工,于是又抽调了一批工人投入灯箱加工,使工作效率提高了50%,结果如期完成工作.
(1)求该公司前5天每天加多少个灯箱;
(2)求规定时间是多少天.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=2,AC=BC= ![]() .
.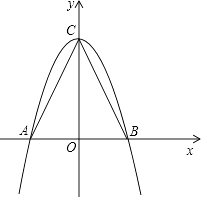
(1)以AB所在的直线为x轴,AB的垂直平分线为y轴,建立直角坐标系如图,请你分别写出A、B、C三点的坐标;
(2)求过A、B、C三点且以C为顶点的抛物线的解析式;
(3)若D为抛物线上的一动点,当D点坐标为何值时,S△ABD= ![]() S△ABC;
S△ABC;
(4)如果将(2)中的抛物线向右平移,且与x轴交于点A′B′,与y轴交于点C′,当平移多少个单位时,点C′同时在以A′B′为直径的圆上(解答过程如果有需要时,请参看阅读材料).
附:阅读材料
一元二次方程常用的解法有配方法、公式法和因式分解法,对于一些特殊方程可以通过换元法转化为一元二次方程求解.如解方程:y4﹣4y2+3=0.
解:令y2=x(x≥0),则原方程变为x2﹣4x+3=0,解得x1=1,x2=3.
当x1=1时,即y2=1,∴y1=1,y2=﹣1.
当x2=3,即y2=3,∴y3= ![]() ,y4=﹣
,y4=﹣ ![]() .
.
所以,原方程的解是y1=1,y2=﹣1,y3= ![]() ,y4=﹣
,y4=﹣ ![]() .
.
再如x2﹣2=4 ![]() ,可设y=
,可设y= ![]() ,用同样的方法也可求解.
,用同样的方法也可求解.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线 ![]() 与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,连接BC.
与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,连接BC.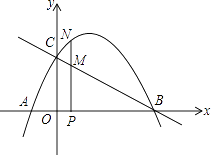
(1)求点A、B、C的坐标.
(2)点P为AB上的动点(点A、O、B除外),过点P作直线PN⊥x轴,交抛物线于点N,交直线BC于点M.设点P到原点的值为t,MN的长度为s,求s与t的函数关系式.
(3)在(2)的条件下,试求出在点P运动的过程中,由点O、P、N围成的三角形与Rt△COB相似时点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com