


|
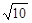

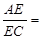
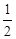 即
即
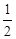 解得t=2
解得t=2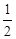 PC×
PC×  AB=
AB=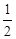 ×2×2="2"
×2×2="2"
|
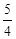 (t+1) ,PC=4-t 若PC="MC" , 则
(t+1) ,PC=4-t 若PC="MC" , 则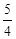 (t+1) =4-t 解得t=
(t+1) =4-t 解得t=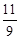



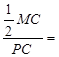
 =
= 解得t=
解得t=

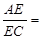
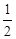 ,从而算出t.再根据相似三角形求出△PEC的高,然后求出△PEC的面积;
,从而算出t.再根据相似三角形求出△PEC的高,然后求出△PEC的面积;

 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源:不详 题型:解答题
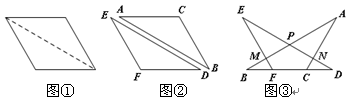
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
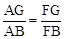 ;②点F是GE的中点;③AF=
;②点F是GE的中点;③AF=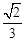 AB;④S△ABC=5S△BDF,其中正确的结论序号是 ▲ .
AB;④S△ABC=5S△BDF,其中正确的结论序号是 ▲ .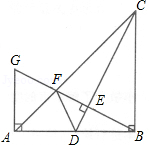
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
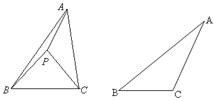
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
 米.同时另一名同学测量一棵树的高度时,发现树的影子不全落在地面上,有一部分影子落在教学楼的墙壁上(如图),其影长为
米.同时另一名同学测量一棵树的高度时,发现树的影子不全落在地面上,有一部分影子落在教学楼的墙壁上(如图),其影长为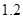 米,落在地面上的影长为
米,落在地面上的影长为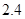 米,则树高为 米.
米,则树高为 米.
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com