
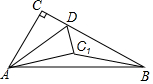
 如图.在Rt△ABC中.∠ACB=90°.∠ABC=30°,AB=6.点D是BC边上一动点,连接AD.将△ACD沿AD折叠.点C落在点C1处.连接C1B.若△BDC1为直角三角形.则BD=2$\sqrt{3}$或3$\sqrt{3}$-3.
如图.在Rt△ABC中.∠ACB=90°.∠ABC=30°,AB=6.点D是BC边上一动点,连接AD.将△ACD沿AD折叠.点C落在点C1处.连接C1B.若△BDC1为直角三角形.则BD=2$\sqrt{3}$或3$\sqrt{3}$-3. 分析 分两种情况进行讨论:当点C1在AB上时,△BDC1为直角三角形;当∠ADC=45°时,△BDC1为直角三角形,分别根据含30°角的直角三角形的性质以及勾股定理进行计算即可.
解答 解:如图所示,当点C1在AB上时,∠AC1D=∠C=90°,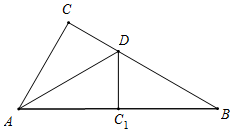
∴∠BC1D=90°,即△BDC1为直角三角形,
∵∠ABC=30°,AB=6,
∴AC=$\frac{1}{2}$AB=3,BD1=2DC1=2CD,
∴BC=$\sqrt{A{B}^{2}-A{C}^{2}}$=3$\sqrt{3}$,
∴BD=$\frac{2}{3}$BC=2$\sqrt{3}$;
如图所示,当∠ADC=45°时,∠CDC1=90°,此时△BDC1为直角三角形,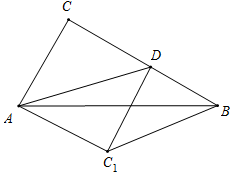
∵∠C=90°,
∴△ACD是等腰直角三角形,
∴CD=AC=3,
而BC=3$\sqrt{3}$,
∴BD=BC-CD=3$\sqrt{3}$-3.
故答案为:2$\sqrt{3}$或3$\sqrt{3}$-3.
点评 本题主要考查了折叠问题以及含30°角的直角三角形的性质的运用,解题时注意:在直角三角形中,30°角所对的直角边等于斜边的一半;翻折变换(折叠问题)实质上就是轴对称变换.


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:初中数学 来源: 题型:选择题
| A. | 10厘米 | B. | 20厘米 | C. | 30厘米 | D. | 40厘米 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 工种 | 工人每月工资(元) | 招聘人数 | 工厂应付工人的约工资(元) |
| A | 3200 | x | 3200x |
| B | 4000 | 120-x | 4000(120-x) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
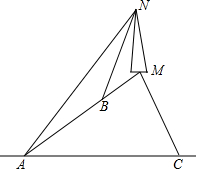 如图所示,在小山顶上有一座信号发射塔MN,在山坡坡脚A处测得塔尖点N的仰角为45°,某人沿坡度为i=1:$\sqrt{3}$坡面上山,行走200米到B处,测得塔尖点N的仰角为60°,已知A,B,M在同一条直线上,求:
如图所示,在小山顶上有一座信号发射塔MN,在山坡坡脚A处测得塔尖点N的仰角为45°,某人沿坡度为i=1:$\sqrt{3}$坡面上山,行走200米到B处,测得塔尖点N的仰角为60°,已知A,B,M在同一条直线上,求:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | k>0,b>0 | B. | k>0,b<0 | C. | k<0,b>0 | D. | k<0,b<0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x≤3 | B. | x≥-$\frac{2}{3}$且x≠3 | C. | x≠-$\frac{2}{3}$ | D. | x≤3且x≠-$\frac{2}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com