
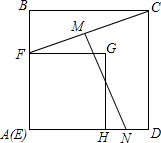
 如图,面积为9cm2的正方形EFGH在面积为25cm2的正方形ABCD所在平面上移动,始终保持EF∥AB,记线段CF的中点为M,DH的中点为N,则线段MN的长度是( )
如图,面积为9cm2的正方形EFGH在面积为25cm2的正方形ABCD所在平面上移动,始终保持EF∥AB,记线段CF的中点为M,DH的中点为N,则线段MN的长度是( )| A. | $\frac{25}{4}$cm | B. | $\frac{73}{4}$cm | C. | $\frac{\sqrt{73}}{2}$cm | D. | $\frac{\sqrt{75}}{2}$cm |
分析 连接HM并延长至点P,使MP=MH,作PQ⊥CD于点Q,连接PC、FH、PD,由△FHM≌△CPM,求出PC=FH=3$\sqrt{3}$,根据等腰直角三角形的性质求出PQ=CQ=3,再运用勾股定理求出PD,根据三角形中位线性质定理可求出MN的长.
解答 解:连接HM并延长至点P,使MP=MH,作PQ⊥CD于点Q,连接PC、FH、PD,
∵正方形EFGH在面积为面积为9cm2,正方形ABCD的面积为25cm2,
∴EF=3,AB=5,
∵M是线段CF的中点,
∴MF=MC,
在△FHM和△CPM中,
$\left\{\begin{array}{l}{MF=MC}\\{∠FMH=∠CMP}\\{MP=MH}\end{array}\right.$,
∴△FHM≌△CPM,
∴FH=PC,∠HFM=∠PCM,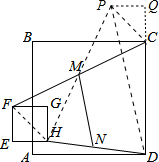
∵EF=EH=3,
∴FH=PC=3$\sqrt{2}$,
∵FG∥BC,
∴∠GFM=∠BCM,
∴∠HFG=∠PCB=45°,
∴∠PCQ=45°,
∴PQ=QC=3,
∴DQ=CD+CQ=8,
∴PD=$\sqrt{73}$,
∵线段HP的中点为M,DH的中点为N,
∴MN=$\frac{1}{2}$PD=$\frac{\sqrt{73}}{2}$.
故选:C.
点评 本题考查了正方形的性质、全等三角形的判定与性质、等腰直角三角形的性质、勾股定理以及三角形中位线性质定理的综合运用,通过辅助线构造全等三角形和三角形中位线是解决问题的关键.


 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案科目:初中数学 来源: 题型:选择题
| A. | 6ab-b=6a | B. | $\frac{1}{a}$+$\frac{1}{b}$=$\frac{2}{a+b}$ | C. | a8÷a2=a4 | D. | (a2b)3=a6b3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
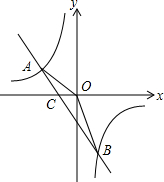 已知反比例函数y=$\frac{{k}_{1}}{3x}$的图象与一次函数y=k2x+m的图象交于A(-1,a),B($\frac{1}{3}$,-3)两点,连结AO.
已知反比例函数y=$\frac{{k}_{1}}{3x}$的图象与一次函数y=k2x+m的图象交于A(-1,a),B($\frac{1}{3}$,-3)两点,连结AO.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
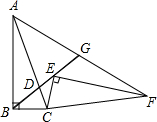 如图,在Rt△ABC中,∠ABC=90°,sin∠BAC=$\frac{1}{3}$,点D是AC上一点,且BC=BD=2,将Rt△ABC绕点C旋转到Rt△FEC的位置,并使点E在射线BD上,连接AF交射线BD于点G.
如图,在Rt△ABC中,∠ABC=90°,sin∠BAC=$\frac{1}{3}$,点D是AC上一点,且BC=BD=2,将Rt△ABC绕点C旋转到Rt△FEC的位置,并使点E在射线BD上,连接AF交射线BD于点G.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
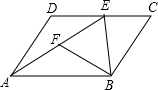 如图,在?ABCD中,过点B作BE⊥DC于点E,连接AE,F为AE上一点,且∠BFE=∠C.
如图,在?ABCD中,过点B作BE⊥DC于点E,连接AE,F为AE上一点,且∠BFE=∠C.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
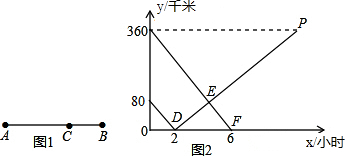
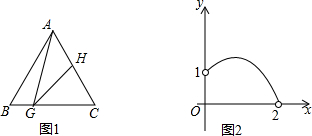 如图1,在等边三角形ABC中,AB=2,G是BC边上一个动点且不与点B、C重合,H是AC边上一点,且∠AGH=30°.设BG=x,图中某条线段长为y,y与x满足的函数关系的图象大致如图2所示,则这条线段可能是图中的( )
如图1,在等边三角形ABC中,AB=2,G是BC边上一个动点且不与点B、C重合,H是AC边上一点,且∠AGH=30°.设BG=x,图中某条线段长为y,y与x满足的函数关系的图象大致如图2所示,则这条线段可能是图中的( )| A. | 线段CG | B. | 线段AG | C. | 线段AH | D. | 线段CH |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com