
【题目】如图,AB是⊙O的直径,点P为AB延长线上一点,PC切⊙O于点C,过点B作BE∥PC交⊙O于点E,连接CE,CB.
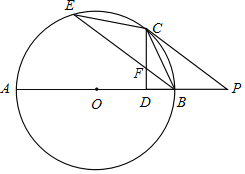
(1)试判断△BCE的形状,并说明理由;
(2)过点C作CD⊥AB于点D交BE于点F,若cosP=![]() ,CF=5,求AB的长.
,CF=5,求AB的长.
【答案】(1)△BCE为等腰三角形,理由见解析;(2)AB=20
【解析】
(1)连接OC,根据切线的性质得到∠OCP=90°,根据平行线的性质得到OC⊥BE,根据等腰三角形的性质即可得到结论;
(2)连接AC,根据圆周角定理得到∠ACB=90°,求得∠A=∠DCB,得到∠FCB=∠CBF,根据等腰三角形的性质得到CF=BF=5,根据勾股定理得到BC=![]() ,由射影定理即可得到结论.
,由射影定理即可得到结论.
(1)△BCE为等腰三角形,
理由:连接OC,
∵PC切⊙O于点C,
∴∠OCP=90°,
∵BE∥PC,
∴OC⊥BE,
∴![]()
∴∠CBE=∠E,
∴EC=BC,
即△BCE是等腰三角形;
(2)连接AC,
∵AB是⊙O的直径,
∴∠ACB=90°,
∵CD⊥AB,
∴∠CDB=90°,
∴∠ACD+∠BCD=∠A+∠ACD=90°,
∴∠A=∠DCB,
∵∠E=∠A,
∴∠FCB=∠CBF,
∴CF=BF=5,
∵BE∥PC,
∴∠DBF=∠P,
∴cosP=cos∠DBF=![]() ,
,
∴BD=4,DF=3,CD=8,
∴BC=![]() ,
,
∵∠ACB=90°,CD⊥AB,
∴BC2=ABBD,
∴(4![]() )2=4AB,
)2=4AB,
∴AB=20.


科目:初中数学 来源: 题型:
【题目】已知在平面直角坐标系中,点![]() ,以线段
,以线段![]() 为直径作圆,圆心为
为直径作圆,圆心为![]() ,直线
,直线![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() .
.
(1)求证:直线![]() 是
是![]() 的切线;
的切线;
(2)点![]() 为
为![]() 轴上任意一动点,连接
轴上任意一动点,连接![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() :
:
①当![]() 时,求所有
时,求所有![]() 点的坐标 (直接写出);
点的坐标 (直接写出);
②求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中(AD>AB),点E是BC上一点,且DE=DA,AF⊥DE,垂足为点F,在下列结论中,不一定正确的是( )
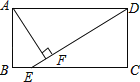
A. △AFD≌△DCE B. AF=![]() AD C. AB=AF D. BE=AD﹣DF
AD C. AB=AF D. BE=AD﹣DF
查看答案和解析>>
科目:初中数学 来源: 题型:
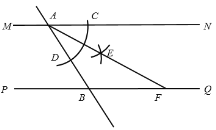
【题目】如图,直线![]() ,直线
,直线![]() 分别与
分别与![]() 、
、![]() 相交于点
相交于点![]() 、
、![]() .小亮同学利用尺规按以下步骤作图:①以点
.小亮同学利用尺规按以下步骤作图:①以点![]() 为圆心,以任意长为半径作弧交
为圆心,以任意长为半径作弧交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ;②分别以
;②分别以![]() 、
、![]() 为圆心,以大于
为圆心,以大于![]() 长为半径作弧,两弧在
长为半径作弧,两弧在![]() 内交于点
内交于点![]() ;③做射线
;③做射线![]() 交
交![]() 于点
于点![]() .若
.若![]() ,
,![]() ,则
,则![]() 的内切圆半径长等于__________.
的内切圆半径长等于__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O直径,CD为弦,AB⊥CD于E,连接CO,AD,∠BAD=20°,下列结论中正确的有( )①CE=OE②∠C=50° ③![]() =
=![]() ④AD=2OE
④AD=2OE
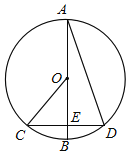
A.①④B.②③C.②③④D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为更精准地关爱留守学生,某学校将留守学生的各种情形分成四种类型:A.由父母一方照看;B.由爷爷奶奶照看;C.由叔姨等近亲照看;D.直接寄宿学校.某数学小组随机调查了一个班级,发现该班留守学生数量占全班总人数的20%,并将调查结果制成如下两幅不完整的统计图.
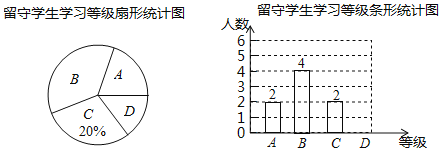
(1)该班共有 名留守学生,B类型留守学生所在扇形的圆心角的度数为 ;
(2)将条形统计图补充完整;
(3)已知该校共有2400名学生,现学校打算对D类型的留守学生进行手拉手关爱活动,请你估计该校将有多少名留守学生在此关爱活动中受益?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与直线
与直线![]() 相交于
相交于![]() ,
,![]() 两点,且抛物线经过点
两点,且抛物线经过点![]()
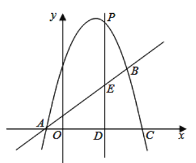
(1)求抛物线的解析式.
(2)点![]() 是抛物线上的一个动点(不与点
是抛物线上的一个动点(不与点![]() 点
点![]() 重合),过点
重合),过点![]() 作直线
作直线![]() 轴于点
轴于点![]() ,交直线
,交直线![]() 于点
于点![]() .当
.当![]() 时,求
时,求![]() 点坐标;
点坐标;
(3)如图所示,设抛物线与![]() 轴交于点
轴交于点![]() ,在抛物线的第一象限内,是否存在一点
,在抛物线的第一象限内,是否存在一点![]() ,使得四边形
,使得四边形![]() 的面积最大?若存在,请求出点
的面积最大?若存在,请求出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
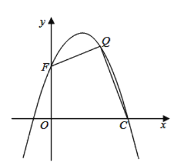
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知x2﹣8x+16﹣m2=0(m≠0)是关于x的一元二次方程
(1)证明:此方程总有两个不相等的实数根;
(2)若等腰△ABC的一边长a=6,另两边长b、c是该方程的两个实数根,求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=6,BC=4,动点Q在边AB上,连接CQ,将△BQC沿CQ所在的直线对折得到△CQN,延长QN交直线CD于点M.
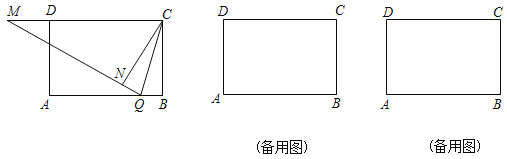
(1)求证:MC=MQ
(2)当BQ=1时,求DM的长;
(3)过点D作DE⊥CQ,垂足为点E,直线QN与直线DE交于点F,且![]() ,求BQ的长.
,求BQ的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com