
分析 (1)根据题意可以得到x的取值范围,从而可以得到铅笔的零售价和批发价;
(2)根据题意可以列出相应的方程,从而可以求得x与m的关系,再根据(1)中x的取值范围和m为正整数,且m2-1>100,可以确定m的值,从而可以得到初三的学生数.
解答 解:(1)由题意可得,
x的取值范围是:240<x≤300(x为正整数);
铅笔的零售价每支应为:$\frac{{m}^{2}-1}{x}$ 元;
铅笔的批发价每支应为:$\frac{{m}^{2}-1}{x+60}$元;
(2)由题意可得,
15×$\frac{{m}^{2}-1}{x}$-15×$\frac{{m}^{2}-1}{x+60}$=1,
化简,得
x2+60x-900(m2-1)=0,
解得,x1=30(m-1),x2=-30(m-1)(舍去),
∴240<30(m-1)≤300,
解得,9<m≤11,
∴m=10或m=11,
当m=10时,m2-1=99<100,故m=10不合题意,舍去,
当m=11时,m2-1=120>100,符合题意,
∴m=11,
∴x=30(m-1)=300,
经检验x=300是原分式方程的解,
答:初三年级共有300名学生,m的值是11.
点评 本题考查一元二次方程的应用,分式方程的应用,解一元一次不等式,解题的关键是明确题意,找出所求问题需要的条件,注意分式方程要检验,应用题最后要作答.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $-\frac{2}{675}$ | B. | $\frac{4}{675}$ | C. | $\frac{2}{675}$或-$\frac{2}{675}$ | D. | $\frac{2}{675}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
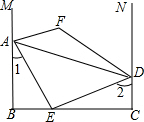 如图,AB⊥BC,AE平分∠BAD交BC于点E,AE⊥DE,∠1+∠2=90°,M、N分别是BA、CD延长线上的点,∠EAM和∠EDN的平分线交于点F.∠F的度数为( )
如图,AB⊥BC,AE平分∠BAD交BC于点E,AE⊥DE,∠1+∠2=90°,M、N分别是BA、CD延长线上的点,∠EAM和∠EDN的平分线交于点F.∠F的度数为( )| A. | 120° | B. | 135° | C. | 150° | D. | 不能确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
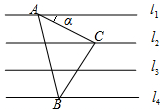 如图,已知直线l1∥l2∥l3∥l4,相邻两条平行线间的距离都相等,如果等腰Rt△ABC(∠ACB=90°)的三个顶点分别在三条直线上,则sinα=$\frac{\sqrt{5}}{5}$.
如图,已知直线l1∥l2∥l3∥l4,相邻两条平行线间的距离都相等,如果等腰Rt△ABC(∠ACB=90°)的三个顶点分别在三条直线上,则sinα=$\frac{\sqrt{5}}{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,点P在△ABC的边AC上,添加一个条件可判断△ABP∽△ACB,其中添加不正确的是( )
如图,点P在△ABC的边AC上,添加一个条件可判断△ABP∽△ACB,其中添加不正确的是( )| A. | ∠ABP=∠C | B. | ∠APB=∠ABC | C. | $\frac{AP}{AB}$=$\frac{AB}{AC}$ | D. | $\frac{AB}{AP}$=$\frac{CB}{BP}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com