
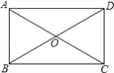
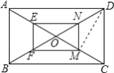
【题目】如图,矩形ABCD的对角线AC,BD相交于点O,点E,F,M,N分别为OA,OB,OC,OD的中点,连接EF,FM,MN,NE.
(1)依题意,补全图形;
(2)求证:四边形EFMN是矩形;
(3)连接DM,若DM⊥AC于点M,ON=3,求矩形ABCD的面积.
【答案】(1)补图见解析;(2)证明见解析;(3) 36![]()
【解析】试题分析:(1)见图形;(2)根据三角形的中位线定理,先证四边形EFMN是平行四边形,再通过对角线相等证明四边形EFMN是矩形;(3)证△OCD是等边三角形。
试题解析:(1)解:如图所示:
(2)证明:∵点E,F分别为OA,OB的中点,∴EF∥AB,EF=![]() AB,
AB,
同理:NM∥CD,MN=![]() DC,∵四边形ABCD是矩形,∴AB∥DC,AB=DC,AC=BD,
DC,∵四边形ABCD是矩形,∴AB∥DC,AB=DC,AC=BD,
∴EF∥NM,EF=MN,∴四边形EFMN是平行四边形,
∵点E,F,M,N分别为OA,OB,OC,OD的中点,∴EO=![]() AO,MO=
AO,MO=![]() CO,
CO,
在矩形ABCD中,AO=CO=![]() AC,BO=DO=
AC,BO=DO=![]() BD,∴EM=EO+MO=
BD,∴EM=EO+MO=![]() AC,
AC,
 同理可证FN=
同理可证FN=![]() BD,∴EM=FN,∴四边形EFMN是矩形.
BD,∴EM=FN,∴四边形EFMN是矩形.
(3)解:∵DM⊥AC于点M,由(2)MO=![]() CO,∴DO=CD,
CO,∴DO=CD,
在矩形ABCD中,AO=CO=![]() AC,BO=DO=
AC,BO=DO=![]() BD,AC=BD,
BD,AC=BD,
∴AO=BO=CO=DO,∴△COD是等边三角形,∴∠ODC=60°,∵MN∥DC,
∴∠FNM=∠ODC=60°,在矩形EFMN中,∠FMN=90°.∴∠NFM=90°﹣∠FNM=30°,
∵NO=3,∴FN=2NO=6,FM=3![]() ,MN=3,∵点F,M分别为OB,OC的中点,
,MN=3,∵点F,M分别为OB,OC的中点,
∴BC=2FM=6![]() ,∴矩形的面积为BCCD=36
,∴矩形的面积为BCCD=36![]() .
.


科目:初中数学 来源: 题型:
【题目】动漫节开幕前,某动漫公司预测某种动漫玩具能够畅销,就分两批分别用32000元和68000元购进了这种玩具销售,其中第二批购进数量是第一批购进数量的2倍,但每套进价多了10元.
(1)该动漫公司这两批各购进多少套玩具?
(2)如果这两批玩具每套售价相同,且全部销售后总利润不少于20000元,那么每套售价至少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学课上,李老师出示了如下框中的题目.
在等边三角形ABC中,点E在AB上,点D在CB的延长线上,且ED=EC,如图.试确定线段AE与DB的大小关系,并说明理由. |
|
小敏与同桌小聪讨论后,进行了如下解答:
(1)特殊情况,探索结论
当点E为AB的中点时,如图1,确定线段AE与的DB大小关系.请你直接写出结论:
AE DB(填“>”,“<”或“=”).

图1 图2
(2)特例启发,解答题目
解:题目中,AE与DB的大小关系是:AE DB(填“>”,“<”或“=”).
理由如下:如图2,过点E作EF∥BC,交AC于点F.
(请你完成以下解答过程)
(3)拓展结论,设计新题
在等边三角形ABC中,点E在直线AB上,点D在直线BC上,且ED=EC.若△ABC的边长为1,AE=2,求CD的长(请你直接写出结果).
查看答案和解析>>
科目:初中数学 来源: 题型:
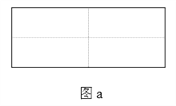
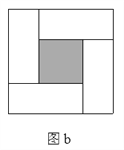
【题目】图a是一个长为2 m、宽为2 n的长方形, 沿图中虚线用剪刀均分成四块小长方形, 然后按图b的形状拼成一个正方形。
(1)你认为图b中的阴影部分的正方形的边长等于多少?
(2)请用两种不同的方法求图中阴影部分的面积。
方法1:
方法2:
(3)观察图b你能写出下列三个代数式之间的等量关系吗?
代数式: ![]()
(4)根据(3)题中的等量关系,解决如下问题:
若![]() ,则
,则![]() = 。
= 。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某人因需要经常去复印资料,甲复印社按A4纸每10页2元计费,乙复印社则按A4纸每10页1元计费,但需按月付一定数额的承包费. 两复印社每月收费情况如图所示,根据图中提供的信息解答下列问题:
(1)乙复印社要求客户每月支付的承包费是 元.
(2)当每月复印 页时,两复印社实际收费相同.
(3)如果每月复印页在250页左右时,应选择哪一个复印社?请简单说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
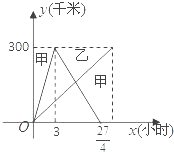
【题目】已知甲. 乙两车分别从相距300km的A. B两地同时出发,相向而行,其中甲到B地后立即返回,下图是它们离各自出发地的距离y(km)与行驶时间x(h)之间的函数图象.
(1)求甲车离出发地的距离y与行驶时间x之间的函数关系式,并写出自变量的取值范围;
(2)当它们行驶到与各自出发地的距离相等时甲用了4.5小时,求乙车离出发地的距离y与行驶时间x之间的函数关系式,并写出x的范围;
(3)在(2)的条件下,求它们的行驶过程中相遇的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两名大学生去距学校36千米的某乡镇进行社会调查.他们从学校出发,骑电动车行驶20分钟时发现忘带相机,甲下车前往,乙骑电动车按原路返回.乙取相机后(在学校取相机所用时间忽略不计),骑电动车追甲.在距乡镇13.5千米处追上甲后同车前往乡镇.乙电动车的速度始终不变.设甲与学校相距y甲(千米),乙与学校相离y乙(千米),甲离开学校的时间为t(分钟).y甲、y乙与x之间的函数图象如图所示,则乙返回到学校时,甲与学校相距________千米.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com