
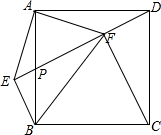
 如图,在正方形ABCD中,点P是AB的中点,连接DP,过点B作BE⊥DP的延长线于点E,连接AE,过点A作AF⊥AE,AF交DP于点F,连接BF、CF.下列结论:
如图,在正方形ABCD中,点P是AB的中点,连接DP,过点B作BE⊥DP的延长线于点E,连接AE,过点A作AF⊥AE,AF交DP于点F,连接BF、CF.下列结论:| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
分析 根据已知和正方形的性质推出∠EAB=∠DAF,∠EBA=∠ADP,AB=AD,证△ABE≌△ADF即可判断①;取EF的中点M,连接AM,推出AM=MF=EM=DF,证∠AMB=∠AMB,BM=BM,AM=MF,推出△ABM≌△FBM即可判断②④;求出∠FDC=∠EBF,推出△BEF≌△DFC即可判断③;证明△AMP≌△BEP,利用线段和差即可判断⑤,可得出答案.
解答  解:
解:
∵正方形ABCD,BE⊥ED,EA⊥FA,
∴AB=AD=CD=BC,∠BAD=∠EAF=90°=∠BEF,
∵∠APD=∠EPB,
∴∠EAB=∠DAF,∠EBA=∠ADP,
在△ABE和△ADF中
$\left\{\begin{array}{l}{∠EAB=∠DAF}\\{AB=AD}\\{∠EBA=∠ADF}\end{array}\right.$
∴△ABE≌△ADF(ASA),
故①正确;
∴AE=AF,BE=DF,
∴∠AEF=∠AFE=45°,
如图,取EF的中点M,连接AM、BM,
∴AM⊥EF,AM=EM=FM,
∴BE∥AM,
∵P为AB中点,
∴AP=BP,
∴AM=BE=DF,
∴∠EMB=∠EBM=45°,
∴∠AMB=90°+45°=135°=∠AMB,
在△ABM和△FBM中
$\left\{\begin{array}{l}{AM=FM}\\{∠AMB=∠FMB}\\{BM=BM}\end{array}\right.$
∴△ABM≌△FBM(SAS),
∴AB=BF,
故②正确;
∴∠BAF=∠BFA,
∴∠BFA≠90°,
故④不正确;
∴∠BAM=∠BFM,
∵∠BEF=90°,AM⊥EF,
∴∠BAM+∠APM=90°,∠EBF+∠EFB=90°,
∴∠APF=∠EBF,
∵AB∥CD,
∴∠APD=∠FDC,
∴∠EBF=∠FDC,且BE=DF,BF=CD,
在△BEF和△DFC中
$\left\{\begin{array}{l}{BE=DF}\\{∠EBF=∠DFC}\\{BF=DC}\end{array}\right.$
∴△BEF≌△DFC(SAS),
∴CF=EF,
故③正确;
在△AMP和△BEP中
$\left\{\begin{array}{l}{∠APM=∠BPE}\\{∠AMP=∠BEP}\\{AP=BP}\end{array}\right.$
∴△AMP≌△BEP(AAS),
∴AM=BE=MF,PM=PE,
∴PF=PM+ME=PE+AM=PE+BE,
故⑤正确;
综上可知正确的结论有①②③⑤,共四个,
故选C.
点评 本题主要考查对正方形的性质,等腰直角三角形,直角三角形斜边上的中线性质,全等三角形的性质和判定,三角形的内角和定理等知识点的理解和掌握,综合运用这些性质进行推理是解此题的关键.


 导学全程练创优训练系列答案
导学全程练创优训练系列答案科目:初中数学 来源: 题型:解答题
 如图,∠1+∠2=180°,∠A=∠C,DA平分∠BDF.
如图,∠1+∠2=180°,∠A=∠C,DA平分∠BDF.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 用水类别 | 现行水价 | 拟调整后水价 |
| 一、居民生活用水 | 0.72 | |
| 1.一户一表 | ||
| 第一阶梯:月用水量在 0~30立方米/户 | 0.82 | |
| 第二阶梯:月用水量超过 30立方米/户 | 1.23 | |
| 2.集体表 | 略 |
| A. |  | B. | 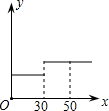 | C. |  | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论正确的( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论正确的( )| A. | abc>0 | |
| B. | 9a+3b+c>0 | |
| C. | a+b≥m(am+b)(m≠1的实数) | |
| D. | 方程ax2+bx+c=2有两个不相等的实数根 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com