
【题目】已知抛物线y=x2-2mx+4m-8的顶点为A
(1) 求证:该抛物线与x轴总有两个交点
(2) 当m=1时,直线BC:y=kx-2与该抛物线交于B、C两点,若线段BC被x轴平分,求k的值
(3) 以A为一个顶点作该抛物线的内接正三角形AMN(M、N两点在抛物线上),请问:△AMN的面积是与m无关的定值吗?若是,请求出这个定值;若不是,请说明理由

【答案】(1)证明见解析(2)k=-1±![]() (3) S△AMN=3
(3) S△AMN=3![]() 为定值
为定值
【解析】试题分析:(1)根据根的判别式可证明交点的个数;
(2)把m=1代入函数的解析式,然后根据二次函数和一次函数的交点,联立方程组,得到含k的关于x的一元二次方程,然后根据根与系数的关系求出k的值;
(3)根据函数和等边三角形的对称性得到AB的关系式,然后根据三角形的面积确定其为定值.
试题解析:(1) ∵△=4m2-4(4m-1)=4(m-2)2+16>0
∴该抛物线与x轴总有两个交点
(2) 当m=1时,y=x2-2x-4
设A(x1,y1)、B(x2,y2)
联立![]() ,整理得x2-(k+2)x-2=0
,整理得x2-(k+2)x-2=0
∴x1+x2=k+2,x1x2=-2
当线段BC被x轴平分时
∴y1+y2=k(x1+x2)-4=0
∴k(k+2)-4=0,解得k=-1±![]()
(3) 根据抛物线和正三角形的对称性,可知MN⊥y轴,设抛物线的对称轴与MN交于点B
则AB=![]() BM
BM
设M(a,b)
∴BM=a-m(m<a)
又AB=yB-yA=b-(4m-8-m2)=a2-2ma+4m-8-(4m-8-m2)=(a-m)2
∴(a-m)2=![]() (a-m),∴a-m=
(a-m),∴a-m=![]()
∴BM=![]() ,AB=3
,AB=3
∴S△AMN=![]() AB·2BM=
AB·2BM=![]() ×3×2×
×3×2×![]() =3
=3![]() 为定值
为定值



 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,AD=2AB,点F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF,CF,则下列结论中一定成立的是____.(把所有正确结论的序号都填在横线上)

①∠DCF=![]() ∠BCD;②EF=CF;③S△BEC=2S△CEF;④∠DFE=3∠AEF.
∠BCD;②EF=CF;③S△BEC=2S△CEF;④∠DFE=3∠AEF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着人民生活水平的不断提高,我市家庭轿车的拥有量逐年增加.据统计,某小区2013年底拥有家庭轿车64辆,2015年底家庭轿车的拥有量达到100辆
(1) 若该小区2013年底到2016年底家庭轿车拥有量的年平均增长率都相同,求该小区到2016年底家庭轿车将达到多少辆?
(2) 为了缓解停车矛盾,该小区决定投资15万元再建造若干个停车位,距测算,建造费用分别为室内车位5000元一个,露天车位1000元一个.考虑到实际因数,计划露天车位的数量不少于室内车位的2倍,且室内的车位不少于19个,求该小区最多可建两种车位各多少个?试写出所有可能的方案
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知∠ABC,∠ACB的平分线交于I.
(1)根据下列条件分别求出∠BIC的度数:
①∠ABC=70°,∠ACB=50°;
②∠ACB+∠ABC=120°;
③∠A=90°;
④∠A=n°.
(2)你能发现∠BIC与∠A的关系吗?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以下列数组作为三角形的三条边长,其中能构成直角三角形的是( )
A. 1, ![]() ,3 B.
,3 B. ![]() ,
, ![]() ,5 C. 1.5,2,2.5 D.
,5 C. 1.5,2,2.5 D. ![]() ,
, ![]() ,
, ![]()
【答案】C
【解析】A、12+(![]() )2≠32,不能构成直角三角形,故选项错误;
)2≠32,不能构成直角三角形,故选项错误;
B、(![]() 2+(
2+(![]() )2≠52,不能构成直角三角形,故选项错误;
)2≠52,不能构成直角三角形,故选项错误;
C、1.52+22=2.52,能构成直角三角形,故选项正确;
D、(![]() ))2+(
))2+(![]() )2≠(
)2≠(![]() )2,不能构成直角三角形,故选项错误.
)2,不能构成直角三角形,故选项错误.
故选:C.
【题型】单选题
【结束】
3
【题目】在Rt△ABC中,∠C=90°,AC=9,BC=12,则点C到斜边AB的距离是( )
(A)![]() (B)
(B)![]() (C)9 (D)6
(C)9 (D)6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,以O为圆心,适当长为半径画弧,交x轴于点M,交y轴于点N,再分别以点M、N为圆心,大于![]() MN的长为半径画弧,两弧在第二象限交于点P.若点P的坐标为(2a,b+1),则a与b的数量关系为( )
MN的长为半径画弧,两弧在第二象限交于点P.若点P的坐标为(2a,b+1),则a与b的数量关系为( )
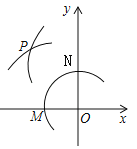
A. a=b B. 2a﹣b=1 C. 2a+b=﹣1 D. 2a+b=1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com