
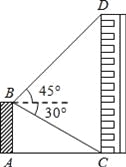
【题目】如图,平台AB高为12m,在B处测得楼房CD顶部点D的仰角为45°,底部点C的俯角为30°,求楼房CD的高度(![]() =1.7).
=1.7).
 全优点练单元计划系列答案
全优点练单元计划系列答案科目:初中数学 来源: 题型:
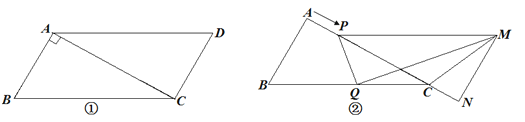
【题目】已知:如图①,在□ABCD中,AB=3cm,BC=5cm,AC⊥AB.△ACD沿AC的方向匀速平移得到△PNM,
速度为1cm/s;同时,点Q从点C出发,沿着CB方向匀速移动,速度为1cm/s;当△PNM停止平移时,
点Q也停止移动,如图②.设移动时间为t (s)(0<t<4).连接PQ、MQ、MC.解答下列问题:
(1)当t为何值时,PQ∥MN?
(2)设△QMC的面积为y(cm2),求y与t之间的函数关系式;
(3)是否存在某一时刻t,使![]() ?若存在,求出t的值;若不存在,请说明理由;
?若存在,求出t的值;若不存在,请说明理由;
(4)是否存在某一时刻t,使PQ⊥MQ?若存在,求出t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
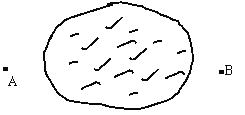
【题目】图为人民公园中的荷花池,现要测量此荷花池两旁A、B两棵树间的距离(我们不能直接量得).请你根据所学知识,以卷尺和测角仪为测量工具设计一种测量方案.
要求:(1)画出你设计的测量平面图;
(2)简述测量方法,并写出测量的数据(长度用![]() …表示;角度用
…表示;角度用![]() …表示);
…表示);
(3)根据你测量的数据,计算A、B两棵树间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB∥CD,CE交AB于点F,若∠E=20°,∠C=45°,则∠A的度数为( )

A. 5° B. 15° C. 25° D. 35°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c和y=max2+mbx+mc,其中a,b,c,m均为正数,且m≠1.则关于这两条抛物线,下列判断正确的是( )
A. 顶点的纵坐标相同 B. 对称轴相同
C. 与y轴的交点相同 D. 其中一条经过平移可以与另一条重合
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com