
【题目】二次函数![]() (
(![]() 是常数,
是常数,![]() )的图象与
)的图象与![]() 轴交于点
轴交于点![]() 和点
和点![]() (点
(点![]() 在点
在点![]() 的右侧),与
的右侧),与![]() 轴交于点
轴交于点![]() ,连接
,连接![]() .
.
(1)用含![]() 的代数式表示点
的代数式表示点![]() 和点
和点![]() 的坐标;
的坐标;
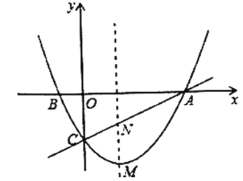
(2)垂直于![]() 轴的直线
轴的直线![]() 在点
在点![]() 与点
与点![]() 之间平行移动,且与抛物线和直线
之间平行移动,且与抛物线和直线![]() 分别交于点
分别交于点![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() ,线段
,线段![]() 的长为
的长为![]() .
.
①当![]() 时,求
时,求![]() 的值;
的值;
②若![]() ,则当
,则当![]() 为何值时,
为何值时,![]() 取得最大值,并求出这个最大值.
取得最大值,并求出这个最大值.
【答案】(1)![]() ,
,![]() ;(2)①3;②当
;(2)①3;②当![]() 时,
时,![]() 取得最大值,最大值为
取得最大值,最大值为![]() .
.
【解析】
(1)纵坐标为0,横坐标为0,将其直接代入二次函数y=![]() (x-5)(x+m)即可求得坐标.
(x-5)(x+m)即可求得坐标.
(2)①求p的值,通常利用表达式表示p,此时p恰为不含字母的式子.因为t=2,此时p=yN-yM,这里yM为点M的纵坐标,yN为点N的纵坐标;
②求最值也要首先表示p,不过发现因为C为抛物线与直线的交点,在-m≤t≤0,p=yM-yN,当0≤t≤5时,p=yN-yM.如此要分开讨论最值,然后再综合在一起,讨论时不要遗漏题目中关于m的限制:0<m≤1.
解:(1)令![]() ,得
,得![]() ,
,
解得:![]() ,
,![]() .
.
∵![]() ,
,
∴![]() .
.
∵点![]() 在点
在点![]() 的右侧,
的右侧,
∴![]() ,
,![]() .
.
令![]() ,得
,得![]() .
.
∴![]() .
.
∴![]() ,
,![]() .
.
(2)①设![]() 的函数关系式为:
的函数关系式为:![]() .
.
把![]() 代入
代入![]() ,解得
,解得![]() ,
,
∴![]() .∵
.∵![]() ,
,
∴点![]() 的纵坐标
的纵坐标![]() ,
,
点![]() 的纵坐标
的纵坐标![]() .
.
∴![]() .
.
②∵点![]() 的横坐标为
的横坐标为![]() ,线段
,线段![]() 的长为
的长为![]() ,
,
∴点![]() 的纵坐标
的纵坐标![]() ,
,
点![]() 的纵坐标
的纵坐标![]() .
.
当![]() 时,
时,![]() .
.
当![]() 时,
时,![]() 取得最大值为
取得最大值为![]() .
.
当![]() 时
时![]() .
.
此二次函数图象开口向上,对称轴为直线![]() ,
,
∴在![]() 时,
时,![]() 随
随![]() 的增大而减小,
的增大而减小,
∴当![]() 时,
时,![]() 取得最大值为
取得最大值为![]() .
.
设![]() ,
,![]() 为对称轴,
为对称轴,
∴当![]() 时,
时,![]() 的值随
的值随![]() 值的增大而增大.
值的增大而增大.
∴![]() 时
时![]() 有最大值3.
有最大值3.
∵![]() ,
,
∴当![]() 时,
时,![]() 取得最大值,最大值为
取得最大值,最大值为![]() .
.


 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案科目:初中数学 来源: 题型:
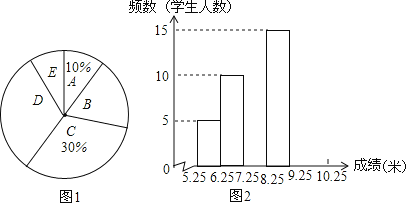
【题目】张老师抽取了九年级部分男生掷实心球的成绩进行整理,分成5个小组(x表示成绩,单位:米).A组:5.25≤x<6.25;B组:6.25≤x<7.25;C组:7.25≤x<8.25;D组:8.25≤x<9.25;E组:9.25≤x<10.25,规定x≥6.25为合格,x≥9.25为优秀.并绘制出扇形统计图和频数分布直方图(不完整).
(1)抽取的这部分男生有______人,请补全频数分布直方图;
(2)抽取的这部分男生成绩的中位数落在_____组?扇形统计图中D组对应的圆心角是多少度?
(3)如果九年级有男生400人,请你估计他们掷实心球的成绩达到合格的有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
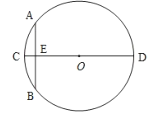
【题目】“圆材埋壁”是我国古代著名的数学著作《九章算术》中的一个问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长六寸,问径几何?”用现代的数学语言表述是:“CD为![]() 的直径,弦
的直径,弦![]() ,垂足为E,CE=1寸,AB=10寸,求直径CD的长”,依题意得CD的长为( )
,垂足为E,CE=1寸,AB=10寸,求直径CD的长”,依题意得CD的长为( )
A.12寸B.13寸C.24寸D.26寸
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线y=﹣![]() x+c与x轴交于点A(4,0),与y轴交于点B,抛物线y=﹣
x+c与x轴交于点A(4,0),与y轴交于点B,抛物线y=﹣![]() x2+bx+c经过A、B两点.
x2+bx+c经过A、B两点.
(1)求抛物线表达式;
(2)点P为抛物线上的一个动点,过点P作垂直于x轴的直线分别交x轴和直线AB于M、N两点,若P、M、N三点中恰有一点是其他两点所连线段的中点(三点重合除外),请求出此时点P的坐标.
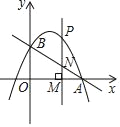
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司有甲种原料![]() ,乙种原料
,乙种原料![]() ,计划用这两种原料生产
,计划用这两种原料生产![]() 、
、![]() 两种产品共40件.生产每件
两种产品共40件.生产每件![]() 种产品需甲种原料
种产品需甲种原料![]() ,乙种原料
,乙种原料![]() ,可获利润900元;生产每件
,可获利润900元;生产每件![]() 种产品需甲种原料
种产品需甲种原料![]() ,乙种原料
,乙种原料![]() ,可获利润1100元.设安排生产
,可获利润1100元.设安排生产![]() 种产品
种产品![]() 件(
件(![]() 为非负整数). .
为非负整数). .
(I)根据题意,填写下表:
甲( | 乙( | 件数(件) | |
|
|
| |
|
|
|
(Ⅱ) 安排生产![]() 、
、![]() 两种产品的件数有几种方案?试说明理由:
两种产品的件数有几种方案?试说明理由:
(Ⅲ) 设生产这批40件产品共可获利润![]() 元,将
元,将![]() 表示为
表示为![]() 的函数,并求出最大利润.
的函数,并求出最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
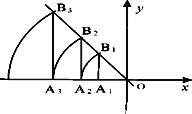
【题目】如图,直线l:y=-![]() x,点A1坐标为(-4,0).过点A1作x轴的垂线交直线l于点B1,以原点O为圆心,OB1长为半径画弧交x轴负半轴于点A2,再过点A2作x轴的垂线交直线l于点B2,以原点O为圆心,OB2长为半径画弧交x轴负半轴于点A3,…,按此做法进行下去,点A2018的坐标为_______.
x,点A1坐标为(-4,0).过点A1作x轴的垂线交直线l于点B1,以原点O为圆心,OB1长为半径画弧交x轴负半轴于点A2,再过点A2作x轴的垂线交直线l于点B2,以原点O为圆心,OB2长为半径画弧交x轴负半轴于点A3,…,按此做法进行下去,点A2018的坐标为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
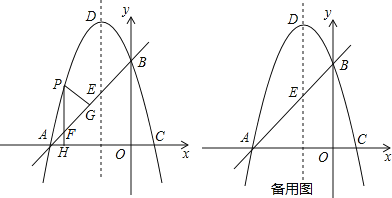
【题目】如图,在平面直角坐标系xoy中,直线y=x+3交x轴于A点,交y轴于B点,过A、B两点的抛物线y=-x2+bx+c交x轴于另一点C,点D是抛物线的顶点.
(1)求此抛物线的解析式;
(2)点P是直线AB上方的抛物线上一点,(不与点A、B重合),过点P作x轴的垂线交x轴于点H,交直线AB于点F,作PG⊥AB于点G.求出△PFG的周长最大值;
(3)在抛物线y=-x2+bx+c上是否存在除点D以外的点M,使得△ABM与△ABD的面积相等?若存在,请求出此时点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在△ABC中,AB=AC,∠BAC=α,直线l经过点A(不经过点B或点C),点C关于直线l的对称点为点D,连接BD,CD.
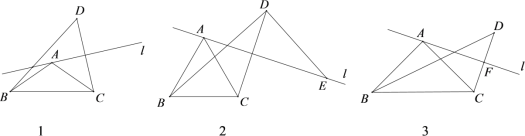
(1)如图1,
①求证:点B,C,D在以点A为圆心,AB为半径的圆上;
②直接写出∠BDC的度数(用含α的式子表示)为 ;
(2)如图2,当α=60°时,过点D作BD的垂线与直线l交于点E,求证:AE=BD;
(3)如图3,当α=90°时,记直线l与CD的交点为F,连接BF.将直线l绕点A旋转的过程中,在什么情况下线段BF的长取得最大值?若AC=2![]() a,试写出此时BF的值.
a,试写出此时BF的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形![]() 中,点
中,点![]() 是边
是边![]() 上一点(不与点
上一点(不与点![]() 重合),点
重合),点![]() 是
是![]() 延长线上一点,且
延长线上一点,且![]() ,连接
,连接![]() .
.
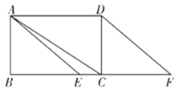
(1)求证:![]()
(2)连接![]() ,其中
,其中![]()
①当四边形![]() 是菱形时,求线段
是菱形时,求线段![]() 与线段
与线段![]() 之间的距离;
之间的距离;
②若点![]() 是
是![]() 的内心,连接
的内心,连接![]() ,直接写出
,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com