
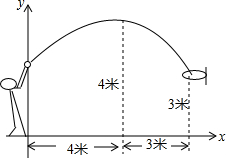
 如图示:学校九年级的一场篮球比赛中,队员甲正在投篮,已知球出手时离地面高为$\frac{20}{9}$米,与篮筐中心的水平距离为7米,当球出手后球与队员甲的水平距离为4米时球达到最大高度4米,设篮球运行的轨迹为抛物线,篮筐距地面3米.
如图示:学校九年级的一场篮球比赛中,队员甲正在投篮,已知球出手时离地面高为$\frac{20}{9}$米,与篮筐中心的水平距离为7米,当球出手后球与队员甲的水平距离为4米时球达到最大高度4米,设篮球运行的轨迹为抛物线,篮筐距地面3米.分析 (1)根据题意得到二次函数的解析式,从而可以求得当x=7时y的值,然后与3比较,即可解答本题;
(2)将x=1代入(1)中求得的解析式,可以得到y的值,然后与3.1比较大小即可解答本题.
解答 解:(1)设抛物线的解析式为:y=a(x-4)2+4,
∵点(0,$\frac{20}{9}$)在此抛物线上,
∴$\frac{20}{9}=a(0-4)^{2}+4$,
解得,a=$-\frac{1}{9}$,
∴y=$-\frac{1}{9}(x-4)^{2}+4$,
当x=7时,y=$-\frac{1}{9}×(7-4)^{2}+4$,得y=3,
即此球能准确投中;
(2)当x=1时,y=$-\frac{1}{9}(1-4)^{2}+4$=3,
∵3.1>3,
∴乙能盖帽成功.
点评 本题考查二次函数的应用,解题的关键是明确题意,找出所求问题需要的条件.


科目:初中数学 来源: 题型:填空题
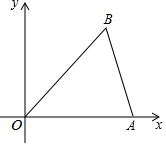 在平面直角坐标系xOy中,点A、B的坐标分别为(3,0)、(2,3),△AB′O′是△ABO关于点A的位似图形,且点O′的坐标为(-1,0),则点B′的坐标为($\frac{5}{3}$,4).
在平面直角坐标系xOy中,点A、B的坐标分别为(3,0)、(2,3),△AB′O′是△ABO关于点A的位似图形,且点O′的坐标为(-1,0),则点B′的坐标为($\frac{5}{3}$,4).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
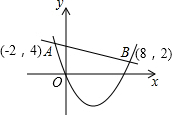 已知二次函数y1=ax2+bx+c (a≠0)与一次函数y2=kx+m(k≠0)的图象相交于点A(-2,4),B(8,2),如图所示,能使y1>y2成立的x取值范围是( )
已知二次函数y1=ax2+bx+c (a≠0)与一次函数y2=kx+m(k≠0)的图象相交于点A(-2,4),B(8,2),如图所示,能使y1>y2成立的x取值范围是( )| A. | x<-2 | B. | -2<x<8 | C. | x>8 | D. | x<-2 或x>8 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
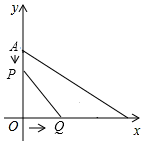 如图,在平面直角坐标系中,已知点A(0,6),B(8,0).点P从A点出发,以每秒1个单位的速度沿AO运动;同时,点Q从O出发,以每秒2个单位的速度沿OB运动,当Q点到达B点时,P、Q两点同时停止运动.
如图,在平面直角坐标系中,已知点A(0,6),B(8,0).点P从A点出发,以每秒1个单位的速度沿AO运动;同时,点Q从O出发,以每秒2个单位的速度沿OB运动,当Q点到达B点时,P、Q两点同时停止运动.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
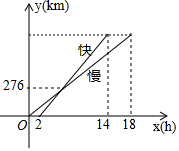 如图是一辆慢车与一辆快车沿相同路线从A地到B地所行的路程与时间之间的函数图象,已知慢车比快车早出发2小时,则A、B两地的距离为828 km.
如图是一辆慢车与一辆快车沿相同路线从A地到B地所行的路程与时间之间的函数图象,已知慢车比快车早出发2小时,则A、B两地的距离为828 km.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com