
·ÖÎö £¨1£©ÀûÓ÷ǸºÊưµÄĐÔÖÊÇó³öbÓëcµÄÖµ£¬¸ù¾Ư¶àÏîʽΪÎå´ÎËÄÏîʽÇó³öaµÄÖµ£»
£¨2£©¢ÙÀûÓõăP¡¢QËù×ߵķ³̀=ACÁĐ³ö·½³̀£»
¢Ú´Ë̀âĐè̉ª·ÖÀà̀ÖÂÛ£ºÏàÓöÇ°ºÍÏàÓöºóÁ½ÖÖÇé¿öÏÂPQ=5ËùĐè̉ªµÄʱ¼ä£®
½â´đ ½â£º£¨1£©¡ß£¨b+3£©2+|c-24|=0£¬
¡àb=-3£¬c=24£¬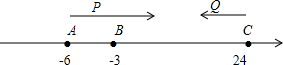
¡ß¶àÏîʽx|a+3|y2-ax3y+xy2-1ÊÇÎå´ÎËÄÏîʽ£¬
¡à|a+3|=5-2£¬-a¡Ù0£¬
¡àa=-6£®
¹Ê´đ°¸ÊÇ£º-6£»-3£»24£»
£¨2£©¢Ù̉À̀ẩâµĂ 3t+7t=|-6-24|=30£¬
½âµĂ t=3£¬
Ộ3t=9£¬
Ëù̉Ô-6+9=3£¬
Ëù̉Ô³ötµÄÖµÊÇ3ºÍµăDËù±íʾµÄÊưÊÇ3£®
¢ÚÉèµăPÔ˶¯xĂëºó£¬P¡¢QÁ½µă¼äµÄ¾àÀëÊÇ5£®
µ±µăPÔÚµăQµÄ×ó±ßʱ£¬3x+5+7£¨x-1£©=30£¬
½âµĂ x=3.2£®
µ±µăPÔÚµăQµÄÓ̉±ßʱ£¬3x-5+7£¨x-1£©=30£¬
½âµĂ x=4.2£®
×ÛÉÏËùÊö£¬µ±µăPÔ˶¯3.2Ăë»̣4.2Ăëºó£¬ƠâÁ½µăÖ®¼äµÄ¾àÀëΪ5¸öµ¥Î»£®
µăÆÀ ±¾̀⿼²éÁË̉»Ôª̉»´Î·½³̀µÄÓ¦ÓĂ£¬½ầâ¹Ø¼üÊÇ̉ª¶Á¶®̀âÄ¿µÄ̉â˼£¬¸ù¾ỪâÄ¿¸ø³öµÄ̀ơ¼₫£¬Ở³öºÏÊʵĵÈÁ¿¹Øϵ£¬ÁĐ³ö·½³̀£¬ÔÙÇó½â£®



| Ä꼶 | ¸ßÖĐ¿Î³̀ | Ä꼶 | ³ơÖĐ¿Î³̀ |
| ¸ß̉» | ¸ß̉»Ăâ·Ñ¿Î³̀ÍƼö£¡ | ³ở» | ³ở»Ăâ·Ñ¿Î³̀ÍƼö£¡ |
| ¸ß¶₫ | ¸ß¶₫Ăâ·Ñ¿Î³̀ÍƼö£¡ | ³ơ¶₫ | ³ơ¶₫Ăâ·Ñ¿Î³̀ÍƼö£¡ |
| ¸ßÈư | ¸ßÈưĂâ·Ñ¿Î³̀ÍƼö£¡ | ³ơÈư | ³ơÈưĂâ·Ñ¿Î³̀ÍƼö£¡ |
¿ÆÄ¿£º³ơÖĐÊưѧ À´Ô´£º ̀âĐÍ£ºÑ¡Ôñ̀â
| A£® | -x2•x6=x8 | B£® | x4¡Âx=x4 | C£® | x2•x4=-x8 | D£® | £¨-x2£©3=-x6 |
²é¿´´đ°¸ºÍ½âÎö>>
¿ÆÄ¿£º³ơÖĐÊưѧ À´Ô´£º ̀âĐÍ£ºÑ¡Ôñ̀â
| A£® | ͬλ½ÇÏàµÈ | B£® | ¶Ô¶¥½ÇÏàµÈ | ||
| C£® | ¶Û½ÇÈư½ÇĐÎÓĐÁ½¸öÈñ½Ç | D£® | Á½Ö±ÏßƽĐĐ£¬ÄÚ´í½ÇÏàµÈ |
²é¿´´đ°¸ºÍ½âÎö>>
¿ÆÄ¿£º³ơÖĐÊưѧ À´Ô´£º ̀âĐÍ£º̀î¿Ờâ
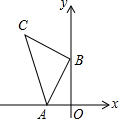 Èçͼ£¬ÔÚƽĂæÖ±½Ç×ø±êϵÖĐ£¬µăAµÄ×ø±êΪ£¨-2£¬0£©£¬µăBµÄ×ø±êΪ£¨0£¬n£©£¬̉ÔµăBΪֱ½Ç¶¥µă£¬µăCÔÚµÚ¶₫ÏóÏ̃ÄÚ£¬×÷µÈÑüÖ±½Ç¡÷ABC£®ỘµăCµÄ×ø±êÊÇ£¨-n£¬2+n£©£®£¨ÓĂ×Öĸn±íʾ£©£®
Èçͼ£¬ÔÚƽĂæÖ±½Ç×ø±êϵÖĐ£¬µăAµÄ×ø±êΪ£¨-2£¬0£©£¬µăBµÄ×ø±êΪ£¨0£¬n£©£¬̉ÔµăBΪֱ½Ç¶¥µă£¬µăCÔÚµÚ¶₫ÏóÏ̃ÄÚ£¬×÷µÈÑüÖ±½Ç¡÷ABC£®ỘµăCµÄ×ø±êÊÇ£¨-n£¬2+n£©£®£¨ÓĂ×Öĸn±íʾ£©£®²é¿´´đ°¸ºÍ½âÎö>>
¿ÆÄ¿£º³ơÖĐÊưѧ À´Ô´£º ̀âĐÍ£º̀î¿Ờâ
²é¿´´đ°¸ºÍ½âÎö>>
¿ÆÄ¿£º³ơÖĐÊưѧ À´Ô´£º ̀âĐÍ£º½â´đ̀â
²é¿´´đ°¸ºÍ½âÎö>>
¿ÆÄ¿£º³ơÖĐÊưѧ À´Ô´£º ̀âĐÍ£ºÑ¡Ôñ̀â
| A£® | x=2 | B£® | x=¡À2 | C£® | x=4 | D£® | x=¡À4 |
²é¿´´đ°¸ºÍ½âÎö>>
¿ÆÄ¿£º³ơÖĐÊưѧ À´Ô´£º ̀âĐÍ£º½â´đ̀â
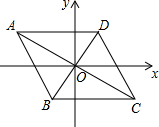 Èçͼ£¬̉ÑÖªµăAµÄ×ø±êΪ£¨-2$\sqrt{3}$£¬2£©£¬µăBµÄ×ø±êΪ£¨-1£¬-$\sqrt{3}$£©£¬ÁâĐÎABCDµÄ¶Ô½ÇÏß½»ÓÚ×ø±êÔµăO£®
Èçͼ£¬̉ÑÖªµăAµÄ×ø±êΪ£¨-2$\sqrt{3}$£¬2£©£¬µăBµÄ×ø±êΪ£¨-1£¬-$\sqrt{3}$£©£¬ÁâĐÎABCDµÄ¶Ô½ÇÏß½»ÓÚ×ø±êÔµăO£®²é¿´´đ°¸ºÍ½âÎö>>
¿ÆÄ¿£º³ơÖĐÊưѧ À´Ô´£º ̀âĐÍ£º½â´đ̀â
²é¿´´đ°¸ºÍ½âÎö>>
°Ù¶ÈÖÂĐÅ - Á·Ï°²áÁбí - ÊỒâÁбí
º₫±±Ê¡»¥ÁªÍøÎ¥·¨ºÍ²»Á¼ĐÅÏ¢¾Ù±¨Æ½̀¨ | ÍøÉÏÓĐº¦ĐÅÏ¢¾Ù±¨×¨Çø | µçĐÅƠ©Æ¾Ù±¨×¨Çø | ÉæÀúÊ·ĐéÎ̃Ö÷̉åÓĐº¦ĐÅÏ¢¾Ù±¨×¨Çø | ÉæÆóÇÖȨ¾Ù±¨×¨Çø
Î¥·¨ºÍ²»Á¼ĐÅÏ¢¾Ù±¨µç»°£º027-86699610 ¾Ù±¨ÓÊÏ䣺58377363@163.com