
| A. | (-m-2n) 2n | B. | (m-2n)(2n-m) | C. | (m-2n)(-m-2n) | D. | (2n-m)(-m-2n) |
分析 A:利用单项式乘以多项式计算;B:提负号后运用完全平方公式计算;C:直接运用平方差公式计算;D:直接运用平方差公式计算.
解答 解:A:(-m-2n) 2n=-2mn-4n2,所以选项A错误;
B:(m-2n)(2n-m)=-(m-2n)2=-m2+4mn-4n2,所以选项B错误;
C:(m-2n)(-m-2n)=-m2+4n2,所以选项C错误;
D:(2n-m)(-m-2n)=m2-4n2,所以选项D正确;
故选D
点评 本题考查了平方差公式和完全平方公式,熟练掌握平方差公式:(a+b)(a-b)=a2-b2和完全平方公式:(a±b)2=a2±2ab+b2;应用公式计算时,应注意以下几个问题:①平方差公式中两个二项式相乘,并且这两个二项式中有一项完全相同,另一项互为相反数;如选项C和D.②完全平方公式:左边是两个数的和的平方;右边是一个三项式,其中首末两项分别是两项的平方,都为正,中间一项是两项积的2倍;其符号与左边的运算符号相同.


 发散思维新课堂系列答案
发散思维新课堂系列答案科目:初中数学 来源: 题型:解答题
 已知点P在一次函数y=kx+b(k,b为常数,且k<0,b>0)的图象上,将点P向左平移1个单位,再向上平移2个单位得到点Q,点Q也在该函数y=kx+b的图象上.
已知点P在一次函数y=kx+b(k,b为常数,且k<0,b>0)的图象上,将点P向左平移1个单位,再向上平移2个单位得到点Q,点Q也在该函数y=kx+b的图象上.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 掷一次骰子,在骰子向上的一面上的点数大于0 | |
| B. | 掷一次骰子,在骰子向上的一面上的点数为7 | |
| C. | 掷三次骰子,在骰子向上的一面上的点数之和刚好为18 | |
| D. | 掷两次骰子,在骰子向上的一面上的点数之积刚好是11 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,直线l1∥l2,直线l与l1、l2分别交于A、B两点,点M、N分别在l1、l2上,点M、N、P均在l的同侧(点P不在l1、l2上),若∠PAM=α,∠PBN=β.
如图,直线l1∥l2,直线l与l1、l2分别交于A、B两点,点M、N分别在l1、l2上,点M、N、P均在l的同侧(点P不在l1、l2上),若∠PAM=α,∠PBN=β.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
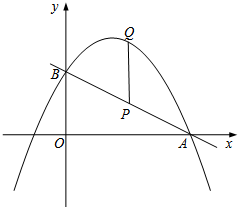 如图,直线y1=kx+2与x轴交于点A(m,0)(m>4),与y轴交于点B,抛物线y2=ax2-4ax+c(a<0)经过A,B两点.P为线段AB上一点,过点P作PQ∥y轴交抛物线于点Q.
如图,直线y1=kx+2与x轴交于点A(m,0)(m>4),与y轴交于点B,抛物线y2=ax2-4ax+c(a<0)经过A,B两点.P为线段AB上一点,过点P作PQ∥y轴交抛物线于点Q.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{3}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com