
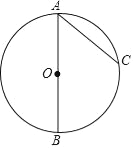
【题目】如图,AB是⊙O的直径,C是⊙O上一点,连接AC.过点B作⊙O的切线,交AC的延长线于点D,在AD上取一点E,使AE=AB,连接BE,交⊙O于点F.
请补全图形并解决下面的问题:
(1)求证:∠BAE=2∠EBD;
(2)如果AB=5,sin∠EBD=![]() .求BD的长.
.求BD的长.
【答案】(1)证明见解析;(2)BD=![]() .
.
【解析】
(1)利用等腰三角形的性质证明∠BAE=2∠BAF,再证明∠EBD=∠BAF即可解决问题;
(2)作EH⊥BD于H.由sin∠BAF=sin∠EBD=![]() ,AB=5,推出BF=
,AB=5,推出BF=![]() ,推出BE=2BF=2
,推出BE=2BF=2![]() ,在Rt△ABF中,EH=BEsin∠EBH=2,推出BH=
,在Rt△ABF中,EH=BEsin∠EBH=2,推出BH=![]() =4,由EH∥AB,推出
=4,由EH∥AB,推出![]() =
=![]() ,由此即可求出DH解决问题;
,由此即可求出DH解决问题;
(1)证明:连接AF.
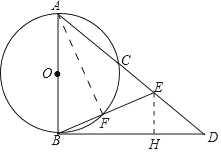
∵AB是直径,
∴∠AFB=90°,
∴AF⊥BE,
∵AB=AE,
∴∠BAE=2∠BAF,
∵BD是⊙O的切线,
∴∠ABD=90°,
∵∠BAF+∠ABE=90°,∠ABF+∠EBD=90°,
∴∠EBD=∠BAF,
∴∠BAE=2∠EBD.
(2)解:作EH⊥BD于H.
∵∠BAF=∠EBD,
∴sin∠BAF=sin∠EBD=![]() ,∵AB=5,
,∵AB=5,
∴BF=![]() ,
,
∴BE=2BF=2![]() ,
,
在Rt△ABF中,EH=BEsin∠EBH=2,
∴BH=![]() =4,
=4,
∵EH∥AB,
∴![]() ,
,
∴![]() ,
,
∴DH=![]() ,
,
∴BD=BH+HD=![]() .
.


 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案科目:初中数学 来源: 题型:
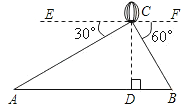
【题目】如图,从热气球C上测得两建筑物A、B底部的俯角分别为30°和60度.如果这时气球的高度CD为90米.且点A、D、B在同一直线上,求建筑物A、B间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等边三角形,BD是中线,延长BC至E,CE=CD,
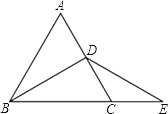
(1)求证:DB=DE
(2)在图中过D作DF⊥BE交BE于F,若CF=4,求△ABC的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
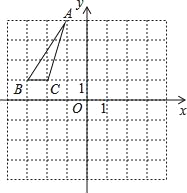
【题目】在如图所示的平面直角坐标系中,△ABC的三个顶点都在小正方形的顶点处,请结合图完成下列各题:
(1)写出tan∠ABC;AB的值;(结果保留根号).
(2)将△ABC绕原点O旋转180°,画出旋转对应的△A′B′C′,并求直线A′C′的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
在数学课上,老师请同学们思考如下问题:
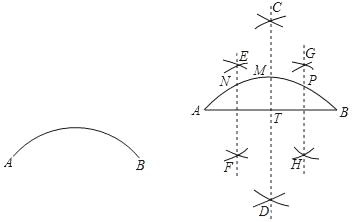
请利用直尺和圆规四等分弧AB.
小亮的作法如下:
如图,
(1)连接AB;
(2)作AB的垂直平分线CD交弧AB于点M.交AB于点T;
(3)分别作线段AT,线段BT的垂直平分线EF,GH,交弧AB于N,P两点;
那么N,M,P三点把弧AB四等分.
老师问:“小亮的作法正确吗?”
请回备:小亮的作法_____(“正确”或“不正确”)理由是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
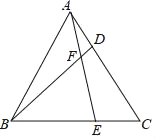
【题目】如图,△ABC是等边三角形,D,E分别是AC,BC边上的点,且AD=CE,连接BD,AE相交于点F.
(1)∠BFE的度数是多少;
(2)如果![]() ,那么
,那么![]() 等于多少;
等于多少;
(3)如果![]() 时,请用含n的式子表示AF,BF的数量关系,并证明.
时,请用含n的式子表示AF,BF的数量关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
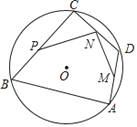
【题目】如图,AB,BC是⊙O的弦,∠B=60°,点O在∠B内,点D为![]() 上的动点,点M,N,P分别是AD,DC,CB的中点.若⊙O的半径为2,则PN+MN的长度的最大值是( )
上的动点,点M,N,P分别是AD,DC,CB的中点.若⊙O的半径为2,则PN+MN的长度的最大值是( )
A. ![]()
B. ![]()
C. ![]()
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,港口A在观测站O的正东方向,OA=4.某船从港口A出发,沿北偏东15°方向航行一段距离后到达B处,此时从观测站O处测得该船位于北偏东60°的方向,则该船航行的距离(即AB的长)为____.

查看答案和解析>>
科目:初中数学 来源: 题型:
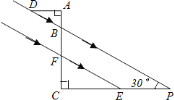
【题目】如图,某一时刻太阳光从教室窗户射入室内,与地面的夹角![]() 为
为![]() ,窗户的一部分在教室地面所形成的影长
,窗户的一部分在教室地面所形成的影长![]() 为
为![]() 米,窗户的高度
米,窗户的高度![]() 为
为![]() 米.求窗外遮阳蓬外端一点
米.求窗外遮阳蓬外端一点![]() 到教室窗户上椽的距离
到教室窗户上椽的距离![]() .(参考数据:
.(参考数据:![]() ,结果精确
,结果精确![]() 米)
米)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com