
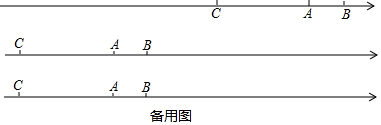
分析 (1)根据非负性即可求出a、b、c的值.
(2)根据甲、乙、丙三个动点的速度求出运行t秒后,甲、乙、丙三个动点对应的位置,根据t>5判断x甲-x乙,x丙-x甲,x丙-x乙与0的大小关系,最后根据绝对值的性质即可化简.
(3)根据甲、乙、丙三个动点的速度求出运行t秒后,甲、乙、丙三个动点对应的位置,根据题意列出方程|x乙-x甲|=|x乙-x丙|,从而求出t的值.
解答 解:(1)由|a-4|+|2a+c|+|b+c-1|=0,
∴a-4=0,2a+c=0,b+c-1=0,
∴a=4,b=9,c=-8
(2)由题可知:甲、乙、丙经过t秒后的路程分别是t,2t,4t,
∵甲、乙、丙三个动点分别从A、B、C三点同时出发沿数轴负方向运动
∴4-x甲=t,9-x乙=2t,-8-x丙=4t,
∴x甲=4-t,x乙=9-2t,x丙=-8-4t,
∴x甲-x乙=t-5,x丙-x甲=-12-3t
x丙-x乙=-17-2t
当t>5时,
x甲-x乙>0,x丙-x甲=-12-3t<-27,x丙-x乙=-17-2t<-27,
∴原式=$\frac{t-5-(-12-3t)+(-17-2t)}{t-5}$=2
(3)由题可知:甲、乙、丙经过t秒后的路程分别是t,2t,4t,
∵甲、乙、丙三个动点分别从A、B、C三点同时出发沿数轴正方向运动,
∴x甲-4=t,x乙-9=2t,x丙+8=4t,
∴x甲=4+t,x乙=9+2t,x丙=-8+4t,
∴x乙-x甲=5+t,x乙-x丙=17-2t
由题意可知:|x乙-x甲|=|x乙-x丙|,
∴(5+t)2=(17-2t)2,
解得:t=4或t=22,
点评 本题考查两点之间的距离,解题的关键是根据题意求出x甲、x乙、x丙的表达式,涉及不等式的性质,解方程,绝对值的性质,本题属于中等题型.


 高中必刷题系列答案
高中必刷题系列答案科目:初中数学 来源: 题型:选择题
| A. | -9+45+28-31 | B. | 31-45-9+28 | C. | 28-9-31-45 | D. | 45-9-28+31 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
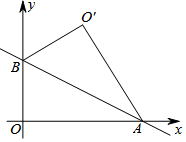 如图,直线y=-$\frac{{\sqrt{3}}}{3}$x+2与x轴,y轴分别交于A,B两点,把△AOB沿着直线AB翻折后得到△AO'B,则点O'的坐标是( )
如图,直线y=-$\frac{{\sqrt{3}}}{3}$x+2与x轴,y轴分别交于A,B两点,把△AOB沿着直线AB翻折后得到△AO'B,则点O'的坐标是( )| A. | $({\sqrt{3}\;,\;\;3})$ | B. | $({3\;,\;\;\sqrt{3}})$ | C. | $({2\;,\;\;2\sqrt{3}})$ | D. | $({2\sqrt{3}\;,\;\;4})$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
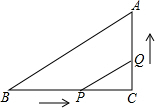 如图所示,∠C=90°,BC=8cm,AC=6cm,点P从点B出发,沿BC向点C以2cm/s的速度移动,点Q从点C出发沿CA向点A以1cm/s的速度移动,如果P、Q分别从B、C同时出发,过多少时,以C、P、Q为顶点的三角形恰与△ABC相似?
如图所示,∠C=90°,BC=8cm,AC=6cm,点P从点B出发,沿BC向点C以2cm/s的速度移动,点Q从点C出发沿CA向点A以1cm/s的速度移动,如果P、Q分别从B、C同时出发,过多少时,以C、P、Q为顶点的三角形恰与△ABC相似?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com