
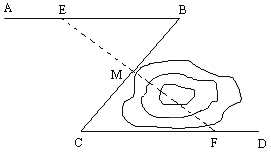
【题目】在新修的花园小区中,有一条“Z”字形绿色长廊ABCD,如图,AB∥CD,在AB、BC、CD三段绿色长廊上各修建一凉亭E、M、F,且BE=CF,M是BC的中点,E、M、F在一条直线上.若在凉亭M与F之间有一池塘,在用皮尺不能直接测量的情况下,你能知道M与F之间的距离吗?试说明理由.
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:初中数学 来源: 题型:
【题目】在正方形ABCD中,BD是一条对角线,点E在直线CD上(与点C,D不重合),连接AE,平移△ADE,使点D移动到点C,得到△BCF,过点F作FG⊥BD于点G,连接AG,EG.

(1)问题猜想:如图1,若点E在线段CD上,试猜想AG与EG的数量关系是____________,位置关系是____________;
(2)类比探究:如图2,若点E在线段CD的延长线上,其余条件不变,小明猜想(1)中的结论仍然成立,请你给出证明;
(3)解决问题:若点E在线段DC的延长线上,且∠AGF=120°,正方形ABCD的边长为2,请在备用图中画出图形,并直接写出DE的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c (a、b、c为常数且a≠0)中的x与y的部分对应值如下表,
x | … | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | … |
y | … | 12 | 5 | 0 | -3 | -4 | -3 | 0 | 5 | 12 | … |
下列四个结论:
(1)二次函数y=ax2+bx+c 有最小值,最小值为-3;
(2)抛物线与y轴交点为(0,-3);
(3)二次函数y=ax2+bx+c 的图像对称轴是x=1;
(4)本题条件下,一元二次方程ax2+bx+c的解是x1=-1,x2=3.
其中正确结论的个数是( )
A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了让学生能更加了解温州历史,某校组织七年级师生共480人参观温州博物馆.学校向租车公司租赁A、B两种车型接送师生往返,若租用A型车3辆,B型车6辆,则空余15个座位;若租用A型车5辆,B型车4辆,则15人没座位.
(1)求A、B两种车型各有多少个座位;
(2)若A型车日租金为350元,B型车日租金为400元,且租车公司最多能提供7辆B型车,应怎样租车能使座位恰好坐满且租金最少,并求出最少租金.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,E是对角线BD上的一点,过点C作CF∥DB,且CF=DE,连接AE,BF,EF.
(1)求证:△ADE≌△BCF;
(2)若∠ABE+∠BFC=180°,则四边形ABFE是什么特殊四边形?说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AE=AC,AB=AD,∠EAB=∠CAD.
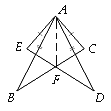
(1)BC与DE相等吗?说明理由.
(2)若BC与DE相交于点F,EF=CF.连接AF,∠BAF与∠DAF相等吗?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,已知一次函数
中,已知一次函数![]() =
=![]() 的图象经过点A(1,0),与反比例函数
的图象经过点A(1,0),与反比例函数![]() =
=![]() (
(![]() >0)的图象相交于点B(m,1).
>0)的图象相交于点B(m,1).
(1)求m的值和一次函数的解析式;
(2)结合图象直接写出:当![]() >0时,不等式
>0时,不等式![]() >
>![]() 的解集.
的解集.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O中,直径CD⊥弦AB于M,AE⊥BD于E,交CD于N,连AC
(1)求证:AC=AN;
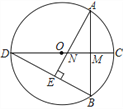
(2)若OM∶OC=3∶5,AB=5,求⊙O的半径;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解
如图 a,在△ABC 中,D 是 BC 的中点.如果用 SABC 表示△ABC 的面积,则由等底等高的三角形的面积相等,可得![]()
![]()
![]()
![]() .同理,如图 b,在 ABC 中,D、E 是 BC 的三等分点,可得
.同理,如图 b,在 ABC 中,D、E 是 BC 的三等分点,可得![]()
![]()
![]()
![]()
![]()

结论应用
已知△ABC 的面积为 42,请利用上面的结论解决下列问题:


(1)如图 1,若 D、E 分别是 AB、AC 的中点,CD 与 BE交于点 F,则△DBF 的面积为 ;
类比推广
(2)如图 2,若 D、E 是 AB 的三等分点,F、G 是 AC 的 三等分点,CD 分别交 BF、BG 于 M、N,CE 分别交 BF、BG 于 P、Q,求△BEP 的面积;
(3)如图2,问题(2)中的条件不变,求四边形EPMD的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com