
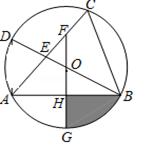
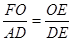 ,然后由O是BD的中点,DA∥OH,可得AD=2OH,则可证得OF•DE=OE•2OH;(2)
,然后由O是BD的中点,DA∥OH,可得AD=2OH,则可证得OF•DE=OE•2OH;(2)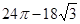
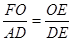 ,然后由O是BD的中点,DA∥OH,可得AD=2OH,则可证得OF•DE=OE•2OH;
,然后由O是BD的中点,DA∥OH,可得AD=2OH,则可证得OF•DE=OE•2OH;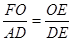 ,求得AD的长,又由在Rt△ABC中,OB=2OH,可求得∠BOH=60°,继而可求得BH的长,又由S阴影=S扇形GOB-S△OHB,即可求得答案.
,求得AD的长,又由在Rt△ABC中,OB=2OH,可求得∠BOH=60°,继而可求得BH的长,又由S阴影=S扇形GOB-S△OHB,即可求得答案.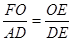 ,即OF•DE=OE•AD
,即OF•DE=OE•AD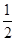 AD=6.
AD=6.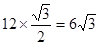



 名师指导一卷通系列答案
名师指导一卷通系列答案科目:初中数学 来源:不详 题型:单选题
 ,则这条弦的中点到弦所对优弧的中点的距离为( )
,则这条弦的中点到弦所对优弧的中点的距离为( )| A.1cm | B.3cm | C.(2+ )cm )cm | D.(2+ )cm )cm |
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
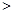 0)在反比例函数
0)在反比例函数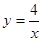 的图象上,则m
的图象上,则m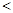 n.其中,正确命题的个数是
n.其中,正确命题的个数是 | A.1个 | B.2个 | C.3个 | D.4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com