

���� ��1��ȡAB���е�M������ME����AM=EC����֤��AME�ա�ECF�����ɵó�AE=EF��
��2����AB��ȡһ��M��ʹAM=EC������ME��֤����AME�ա�BCF���Ӷ��ɵõ�AE=EF��
��3����BA���ӳ�����ȡһ��N��ʹAN=CE������NE��Ȼ��֤����ANE�ա�ECF���Ӷ��ɵõ�AE=EF��
���  �⣺��1����ȷ���������£�
�⣺��1����ȷ���������£�
ȡAB���е�M������ME��
��AM=BM=$\frac{1}{2}$AB��
��AD=AB=BC=DC��
���ı���ABCD�����Σ�
�ߡ�B=90�㣬
���ı���ABCD�������Σ�
���BCD=90�㣬
���DCG=90�㣬
��CFƽ�֡�DCG��
���DCF=45�㣬
���ECF=90��+45��=135�㣬
�ߡ�AEF=90�㣬
���AEB+��FEC=90�㣬
�ߡ�BAE+��AEB=90�㣬
���BAE=��FEC��
�ߵ�E�DZ�BC���е㣬
��BE=EC=$\frac{1}{2}$BC��
��AM=EC=BM=BE��
���BME�ǵ���ֱ�������Σ�
���BME=45�㣬
���AME=135��=��ECF��
�ڡ�AME�͡�ECF�У�$\left\{\begin{array}{l}{��BAE=��CEF}&{\;}\\{AM=EC}&{\;}\\{��AME=��ECF}&{\;}\end{array}\right.$��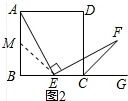
���AME�ա�ECF��ASA����
��AE=EF
��2����ȷ���������£���AB��ȡһ��M��ʹAM=EC������ME��
��AB=BC��AM=EC��
��BM=BE��
���BME=45�㣮
���AME=135�㣮
��CF�����ƽ���ߣ�
���DCF=45�㣬
���ECF=135�㣮
���AME=��ECF��
�ߡ�AEB+��BAE=90�㣬��AEB+��CEF=90�㣬
���BAE=��CEF��
�ڡ�AME�͡�ECF�У�$\left\{\begin{array}{l}{��AME=��ECF}&{\;}\\{AM=EC}&{\;}\\{��MAE=��CEF}&{\;}\end{array}\right.$��
���AME�ա�BCF��
��AE=EF��
��3����ȷ���������£���BA���ӳ�����ȡһ��N��ʹAN=CE������NE��
��AB=BC��AN=CE��
��BN=BE��
���N=��FCE=45�㣮��
���ı���ABCD�������Σ�
��AD��BE��
���DAE=��BEA��
���NAE=��CEF��
�ڡ�ANE�͡�ECF�У�$\left\{\begin{array}{l}{��N=��FCE}&{\;}\\{AN=CE}&{\;}\\{��NAE=��CEF}&{\;}\end{array}\right.$��
���ANE�ա�ECF��ASA����
��AE=EF��
���� �������������ۺ���Ŀ���������ȫ�������ε����ʺ��ж��������ε��ж������ʡ�����ֱ�������ε��ж������ʵ�֪ʶ�����մ������⸨���ߵ������ǽ���Ĺؼ���


 ǧ�������������ĩ�����Ծ�����ϵ�д�
ǧ�������������ĩ�����Ծ�����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\sqrt{��sin��-1��^{2}}$=sin��-1 | B�� | tan��90��-����=cot�� | ||
| C�� | cos60��=2cos30�� | D�� | cot90��=cot30��+cot60�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����֪����ABCD�������Խ��߳��ֱ���6��8����M��N�ֱ��DZ�BC��AB�ϵĶ��㣬�ڶԽ���AC����һ��P��ʹPM+PN����Сֵ������Сֵ��$\frac{24}{5}$��
��ͼ����֪����ABCD�������Խ��߳��ֱ���6��8����M��N�ֱ��DZ�BC��AB�ϵĶ��㣬�ڶԽ���AC����һ��P��ʹPM+PN����Сֵ������Сֵ��$\frac{24}{5}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� |  | B�� |  | C�� |  | D�� |  |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| x | 1 | 2 | 3 | 4 | �� |
| y | 2 | 5 | 10 | 17 | �� |
| A�� | y=x+1 | B�� | y=2x+1 | C�� | y=2x-1 | D�� | y=x2+1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
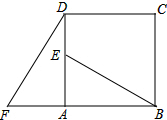 ��ͼ���ı���ABCD�������Σ���ADF��תһ���ǶȺ�õ���ABE�����AF=4��AB=7��
��ͼ���ı���ABCD�������Σ���ADF��תһ���ǶȺ�õ���ABE�����AF=4��AB=7���鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com