【题目】如图，在边长为10的正方形ABCD中，△PAQ是正三角形，求PB的长．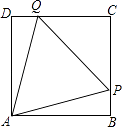 
【答案】解：设PB=x， ∴PC=10﹣x，
由题意可知：AD=AB，AQ=AP
在Rt△AQD与Rt△APB中，
∴Rt△AQD≌Rt△APB（HL）
∴DQ=PB=x，
∴CQ=10﹣x，
在Rt△APB中，AP2=100+x2 ，
在Rt△CQP中，AP2=CQ2+PC2 ，
∴100+x2=2（10﹣x）2
化简：x2﹣40x+100=0，
解得：x=20±10 
，
∵x＜10，
∴PB=x=20﹣10
【解析】设PB=x，根据正方形以及等边三角形的性质求出PQ与PC的表达式，然后利用勾股定理列出方程求出x的值．
【考点精析】解答此题的关键在于理解等边三角形的性质的相关知识，掌握等边三角形的三个角都相等并且每个角都是60°，以及对正方形的性质的理解，了解正方形四个角都是直角，四条边都相等；正方形的两条对角线相等，并且互相垂直平分，每条对角线平分一组对角；正方形的一条对角线把正方形分成两个全等的等腰直角三角形；正方形的对角线与边的夹角是45o；正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形．
口算题天天练系列答案科目：初中数学 来源： 题型：
【题目】Rt△ABC中，∠C=90°，点D、E分别是△ABC边AC、BC上的点，点P是一动点．令∠PDA=∠1，∠PEB=∠2，∠DPE=∠α．
（1）若点P在线段AB上，如图（1）所示，且∠α=50°，则∠1+∠2= °；
（2）若点P在边AB上运动，如图（2）所示，则∠α、∠1、∠2之间有何关系？说明理由．
（3）若点P在Rt△ABC斜边BA的延长线上运动（CE＜CD），则∠α、∠1、∠2之间有何关系？猜想并说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】九年级数学兴趣小组经过市场调查，得到某种运动服每月的销量与售价的相关信息如下表：
售价（元/件） | 100 | 110 | 120 | 130 | … |
月销量（件） | 200 | 180 | 160 | 140 | … |
已知该运动服的进价为每件60元，设售价为x元．
（1）请用含x的式子表示：①销售该运动服每件的利润是 （）元；②月销量是 （）件；（直接写出结果）
（2）设销售该运动服的月利润为y元，那么售价为多少时，当月的利润最大，最大利润是多少？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知矩形ABCD，AB=6，BC=8，E，F分别是AB，BC的中点，AF与DE相交于I，与BD相交于H，则四边形BEIH的面积为（ ）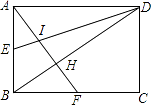 
A.
B.
C.
D.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】小红的奶奶开了一个金键牛奶销售店，主要经营“金键学生奶”、“金键酸牛奶”、“金键原味奶”，由于经营不善，经常导致牛奶滞销（没卖完）或脱销（量不够），为此细心的小红结合所学知识帮奶奶统计了一个星期牛奶的销售情况，并绘制成下表：
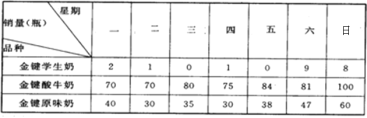
（1）计算各品种牛奶的日平均销售量，并说明哪种牛奶销量最高；
（2）计算各品种牛奶的方差（保留两位小数），并比较哪种牛奶销量最稳定；
（3）假如你是小红，会给奶奶哪些建议?
查看答案和解析>>
科目：初中数学 来源： 题型：
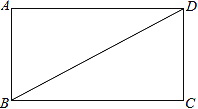
【题目】如图，BD是矩形ABCD的一条对角线．
（1）作BD的垂直平分线EF，分别交AD、BC于点E、F，垂足为点O（用尺规作图，保留作图痕迹，不要求写作法）；
（2）求证：AF=CE．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】(1)如图①，你知道∠BOC＝∠B＋∠C＋∠A的奥秘吗？请用你学过的知识予以证明；
(2)如图②，设x＝∠A＋∠B＋∠C＋∠D＋∠E，运用(1)中的结论填空．
x＝____________°；x＝____________°；x＝____________°；
(3)如图③，一个六角星，其中∠BOD＝70°，则∠A＋∠B＋∠C＋∠D＋∠E＋∠F＝________°.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在一次“寻宝”人找到了如图所示的两个标志点A（2，3），B（4，1），A，B两点到“宝藏”点的距离都是
，则“宝藏”点的坐标是（ ）
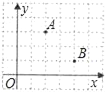
A. （1，0） B. （5，4） C. （1，0）或（5，4） D. （0，1）或（4，5）
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
