
分析 根据a、b互为相反数,可得a+b=0;根据c、d互为倒数,可得cd=1;根据x的绝对值是2,可得x2=22=4,据此求出$\frac{a+b}{x}$+x2-cd的值是多少即可.
解答 解:∵a、b互为相反数,
∴a+b=0;
∵c、d互为倒数,
∴cd=1;
∵x的绝对值是2,
∴x2=22=4,
∴$\frac{a+b}{x}$+x2-cd
=0+4-1
=3
故答案为:3.
点评 此题主要考查了代数式求值问题,要熟练掌握,求代数式的值可以直接代入、计算.如果给出的代数式可以化简,要先化简再求值.题型简单总结以下三种:①已知条件不化简,所给代数式化简;②已知条件化简,所给代数式不化简;③已知条件和所给代数式都要化简.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| x | 6.17 | 6.18 | 6.19 | 6.20 |
| y=ax2+bx+c | -0.03 | -0.01 | 0.02 | 0.06 |
| A. | -0.01-0.02之间 | B. | 0.02-0.06之间 | C. | 6.17-6.18之间 | D. | 6.18-6.19之间 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
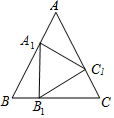 如图,等边三角形的边长为3,依次在AB、BC、AC上取点A1、B1、C1,使AA1=BB1=CC1=1,则△A1B1C1的面积是$\frac{3}{4}\sqrt{3}$.
如图,等边三角形的边长为3,依次在AB、BC、AC上取点A1、B1、C1,使AA1=BB1=CC1=1,则△A1B1C1的面积是$\frac{3}{4}\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
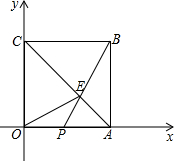 如图,在平面直角坐标系中,点0是坐标原点.边长为6的正方形OABC的顶点A,C分别在x轴和y轴的正半轴上,点E是对角线AC上一点,连接OE、BE,BE的延长线交OA于点P,若△OCE的面积为12.
如图,在平面直角坐标系中,点0是坐标原点.边长为6的正方形OABC的顶点A,C分别在x轴和y轴的正半轴上,点E是对角线AC上一点,连接OE、BE,BE的延长线交OA于点P,若△OCE的面积为12.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com