
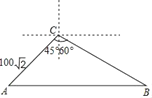
【题目】在某校组织的“交通安全宣传教育月”活动中,八年级数学兴趣小组的同学进行了如下的课外实践活动.具体内容如下:在一段笔直的公路上选取两点A、B,在公路另一侧的开阔地带选取一观测点C,在C处测得点A位于C点的南偏西45°方向,且距离为100![]() 米,又测得点B位于C点的南偏东60°方向.已知该路段为乡村公路,限速为60千米/时,兴趣小组在观察中测得一辆小轿车经过该路段用时13秒,请你帮助他们算一算,这辆小车是否超速?(参考数据:
米,又测得点B位于C点的南偏东60°方向.已知该路段为乡村公路,限速为60千米/时,兴趣小组在观察中测得一辆小轿车经过该路段用时13秒,请你帮助他们算一算,这辆小车是否超速?(参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73,计算结果保留两位小数)
≈1.73,计算结果保留两位小数)
【答案】小车的速度为21米/秒;时速为75.6千米/时>60千米/时,所以超速了.
【解析】
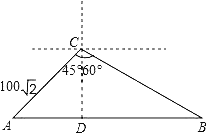
作CD⊥AB于点D,据题意可得∠A=45°,∠CBD=30°,在Rt△ADC和Rt△CDB中,分别求出AD和BD的值,则AB可求,进而可求小轿车经过该路段的速度,与限速60千米/时作比较即得结论.
解:如图,作CD⊥AB于点D.
∵在Rt△ADC中,∠ACD=45°,AC=100![]() ,
,
∴CD=ACcos∠ACD=![]() AC=100,
AC=100,
∴AD=CD=100.
∵在Rt△CDB中,∠BCD=60°,
∴∠CBD=30°,
∴BD=![]() CD=100
CD=100![]() .
.
∴AB=AD+BD=100+100![]() =100(
=100(![]() +1)≈273.
+1)≈273.
又∵小轿车经过AB路段用时13秒,
∴小轿车的速度为![]() =21米/秒.
=21米/秒.
而该路段限速为60千米/时≈16.67米/秒,
∵21>16.67,
∴这辆小轿车超速了.


科目:初中数学 来源: 题型:
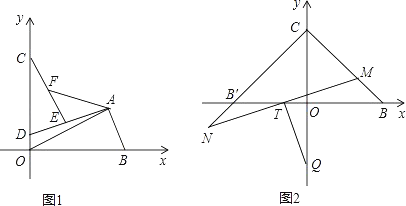
【题目】如图,直角坐标系中,点B(a,0),点C(0,b),点A在第一象限.若a,b满足(a﹣t)2+|b﹣t|=0(t>0).
(1)证明:OB=OC.
(2)如图1,连接AB,过A作AD⊥AB交y轴于D,在射线AD上截取AE=AB,连接CE,F是CE的中点,连接AF,OA,当点A在第一象限内运动(AD不过点C)时,证明:∠OAF的大小不变.
(3)如图2,B′与B关于y轴对称,M在线段BC上,N在CB′的延长线上,且BM=NB′,连接MN交x轴于点T,过T作TQ⊥MN交y轴于点Q,求点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“中国梦”是中华民族每个人的梦,也是每个中小学生的梦.各中小学开展经典诵读活动,无疑是“中国梦”教育这一宏大乐章里的响亮音符.某中学在全校800名学生中随机抽取部分学生进行调查,调查内容分为四种:![]() :非常喜欢,
:非常喜欢,![]() :喜欢,
:喜欢,![]() :一般,
:一般,![]() :不喜欢
:不喜欢
被调查的同学只能选取其中的一种.根据调查结果,绘制出两个不完整的统计图(图形如下),并根据图中信息,回答下列问题:
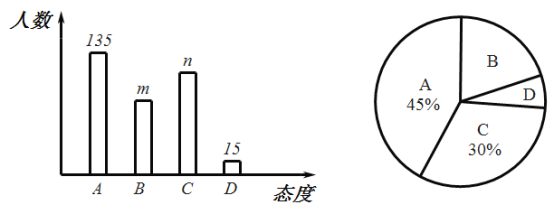
(1)本次调查中,一共调查了多少名学生?
(2)条形统计图中,![]() _________,
_________,![]() _____________;
_____________;
(3)在扇形统计图中,“![]() :喜欢”所在扇形的圆心角的度数是多少?
:喜欢”所在扇形的圆心角的度数是多少?
(4)请估计该学校800名学生中“![]() :非常喜欢”和“
:非常喜欢”和“![]() :喜欢”经典诵读的学生共有多少人?
:喜欢”经典诵读的学生共有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某广场一灯柱AB被一钢缆CD固定,CD与地面成40°夹角,且CB=5米.

(1)求钢缆CD的长度;(精确到0.1米)
(2)若AD=2米,灯的顶端E距离A处1.6米,且∠EAB=120°,则灯的顶端E距离地面多少米?
(参考数据:tan400=0.84, sin400=0.64, cos400=![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列计算过程,猜想立方根.
![]() =1
=1 ![]() =8
=8 ![]() =27
=27 ![]() =64
=64 ![]() =125
=125 ![]() =216
=216 ![]() =343
=343 ![]() =512
=512 ![]() =729
=729
(1)小明是这样试求出19683的立方根的,先估计19683的立方根的个位数, 猜想它的个位数为 , 又由![]() <19000<
<19000< ![]() ,猜想19683的立方根十位数为 ,验证得19683的立方根是 .
,猜想19683的立方根十位数为 ,验证得19683的立方根是 .
(2)请你根据(1)中小明的方法,完成如下填空:
① ![]() = ; ②
= ; ②![]() = ;③
= ;③![]() = .
= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】结合图形填空:
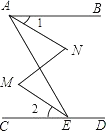
已知,如图,∠BAE+∠AED=180°,∠M=∠N,试说明:∠1=∠2.
解:∵∠BAE+∠AED=180°
∴ AB∥CD( )
∴∠BAE= ( )
又∵∠M=∠N (已知)
∴ AN∥ ( )
∴∠NAE= (两直线平行,内错角相等)
∴∠BAE﹣∠NAE= ﹣
即∠1=∠2.( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】潮州旅游文化节开幕前,某凤凰茶叶公司预测今年凤凰茶叶能够畅销,就用32000元购进了一批凤凰茶叶,上市后很快脱销,茶叶公司又用68000元购进第二批凤凰茶叶,所购数量是第一批购进数量的2倍,但每千克凤凰茶叶进价多了10元.
(1)该凤凰茶叶公司两次共购进这种凤凰茶叶多少千克?
(2)如果这两批茶叶每千克的售价相同,且全部售完后总利润率不低于20%,那么每千克售价至少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》是我国古代数学的经典著作,书中有一个问题:“今有黄金九枚,白银一十一枚,称之重适等.交易其一,金轻十三两.问金、银一枚各重几何?”.意思是:甲袋中装有黄金9枚(每枚黄金重量相同),乙袋中装有白银11枚(每枚白银重量相同),称重两袋相等.两袋互相交换1枚后,甲袋比乙袋轻了13两(袋子重量忽略不计).问黄金、白银每枚各重多少两?设每枚黄金重x两,每枚白银重y两,根据题意得( )
A. ![]()
B. ![]()
C. ![]()
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com