
【题目】如图,长方形AOBC,以O为坐标原点,OB、OA分别在x轴、y轴上,点A的坐标为(0,8),点B的坐标为(10,0),点E是BC边上一点,把长方形AOBC沿AE翻折后,C点恰好落在x轴上点F处.
(1)求点E、F的坐标;
(2)求AF所在直线的函数关系式;
(3)在x轴上求一点P,使△PAF成为以AF为腰的等腰三角形,请直接写出所有符合条件的点P的坐标.

【答案】(1)(6,0),(10,3);(2)![]() ;(3)(-6,0),(-4,0),(16,0).
;(3)(-6,0),(-4,0),(16,0).
【解析】
(1)易证:ACEAFE,得:AF=AC=10,根据勾股定理,分别求出OF和BE,即可得到答案;
(2)设AF所在直线的函数解析式为:y=kx+b,根据待定系数法,即可求解;
(3)分3种情况:①当AF=AP时,②当AF=PF时,③当AF=PF时,分别求出点P的坐标.
(1)∵长方形AOBC,以O为坐标原点,OB、OA分别在x轴、y轴上,点A的坐标为(0,8),点B的坐标为(10,0),
∴AC=OB=10,BC=OA=8,
∵长方形AOBC沿AE翻折后,C点恰好落在x轴上点F处,
∴ACEAFE,
∴AF=AC=10,
∵在RtAOF中,![]() ,
,
∴![]() ,
,
∴点F坐标是:(6,0),BF=10-6=4,
设BE=x,则FE=CE=8-x,
∵在RtBEF中,![]() ,
,
∴![]() ,解得:x=3,
,解得:x=3,
∴点E的坐标是:(10,3)
(2)设AF所在直线的函数解析式为:y=kx+b,
把A(0,8),F(6,0),代入y=kx+b,得:![]() ,解得:
,解得: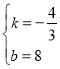
∴AF所在直线的函数解析式为:![]() ;
;
(3)①当AF=AP时,如图1,则OP=OF=6,
∴点P坐标是:(-6,0),
②当AF=PF时,如图2,则PF=10,OP=PF-OF=10-6=4,
∴点P坐标是:(-4,0),
③当AF=PF时,如图3,则PF=10,OP=PF+OF=10+6=16,
∴点P坐标是:(16,0),
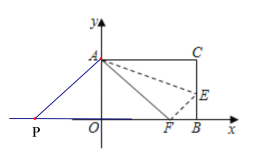

图1 图2

图3


科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,在边长为
,在边长为![]() 的小正方形组成的网格中,
的小正方形组成的网格中,![]() 的顶点
的顶点![]() 、
、![]() 均在格点上,点
均在格点上,点![]() 在
在![]() 轴上,点
轴上,点![]() 的坐标为
的坐标为![]() .
.

![]() 点
点![]() 关于点
关于点![]() 中心对称的点的坐标为________;
中心对称的点的坐标为________;
(2)![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 后得到
后得到![]() ,那么点
,那么点![]() 的坐标为________;线段
的坐标为________;线段![]() 在旋转过程中所扫过的面积是________.
在旋转过程中所扫过的面积是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2017浙江省湖州市)如图,已知∠AOB=30°,在射线OA上取点O1,以O1为圆心的圆与OB相切;在射线O1A上取点O2,以O2为圆心,O2O1为半径的圆与OB相切;在射线O2A上取点O3,以O3为圆心,O3O2为半径的圆与OB相切;…;在射线O9A上取点O10,以O10为圆心,O10O9为半径的圆与OB相切.若⊙O1的半径为1,则⊙O10的半径长是______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,半圆O的直径DE=12 cm,在△ABC中,∠ACB=90°,∠ABC=30°,BC=12 cm.半圆O以2 cm/s的速度自左向右运动,在运动过程中,点D,E始终在直线BC上.设运动时间为t s,当t=0时,半圆O在△ABC的左侧,OC=8 cm.
(1)当t=________s时,半圆O与AC所在直线第一次相切;点C到直线AB的距离为________.
(2)当t为何值时,直线AB与半圆O所在的圆相切?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,△ABC是等腰三角形,AB=AC,点D,E,F分别在AB,BC,AC边上,且BD=CE,BE=CF.
(1)求证:△DEF是等腰三角形;
(2)猜想:当∠A满足什么条件时,△DEF是等边三角形?并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠C=90°,D是边BC上一点,连接AD,若∠BAD+3∠CAD=90°,DC=a,BD=b,则AB=________. (用含a,b的式子表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】三个小岛![]() 、
、![]() 、
、![]() 的位置如图所示,在
的位置如图所示,在![]() 处测得小岛
处测得小岛![]() 在
在![]() 的北偏东
的北偏东![]() 方向,在
方向,在![]() 处测得小岛
处测得小岛![]() 在
在![]() 的北偏东
的北偏东![]() 方向,且
方向,且![]() 、
、![]() 之间的距离是
之间的距离是![]() 海里,求:小岛
海里,求:小岛![]() 在小岛
在小岛![]() 的正东方向多少海里?(精确到
的正东方向多少海里?(精确到![]() 海里)(参考数据:
海里)(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com