Question

3．如图，直线AB∥CD

（1）在图1中，∠BME，∠E，∠END的数量关系为：∠E=∠BME+∠END（直接写出结论）
（2）在图2中，∠BMF，∠F，∠FND的数量关系为：∠BMF=∠F+∠FND（直接写出结论）
（3）如图3，NE平分∠FND，MB平分∠FME，且∠E-∠F=60°，求∠FND的大小．

Answer 1

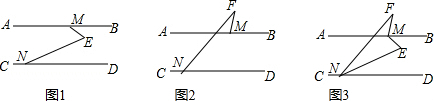
分析 （1）过点E作EF∥AB，根据两直线平行，内错角相等可得∠BME=∠1，∠END=∠2，然后相加即可得解；
（2）先根据两直线平行，同位角相等求出∠3=∠FND，再根据三角形的一个外角等于与它不相邻的两个内角的和列式计算即可得解；
（3）设∠END=x°，∠BME=y°，根据（1）的结论可得x+y=∠E，根据（2）的结论可得2x+∠F=y，然后消掉y并表示出x，再根据∠E-∠F=60°，求出x，然后根据角平分线的定义求解即可；

解答 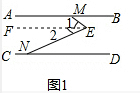解：（1）如图1，过点E作EF∥AB，
∵AB∥CD，
∴AB∥EF∥CD，
∴∠BME=∠1，∠END=∠2，
∴∠1+∠2=∠BME+∠END，
即∠E=∠BME+∠END，
故答案为：∠E=∠BME+∠END；

（2）如图2，∵AB∥CD，
∴∠3=∠FND，
∴∠BMF=∠F+∠3=∠F+∠FND，
即∠BMF=∠F+∠FND；，
故答案为：∠BMF=∠F+∠FND；

（2）如图3，设∠END=x°，∠BME=y°，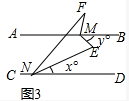
由（1）的结论可得x+y=∠E，2x+∠F=y，
消掉x得，3x=∠E-∠F，
∵∠E-∠F=60，
∴3x=60°，
解得x=20°，
∵NE平分∠FND，
∴∠FND=2x=2×20°=40°．

点评 本题考查了平行线的性质，三角形的一个外角等于与它不相邻的两个内角的和的性质，角平分线的定义，此类题目，过拐点作平行线是解题的关键，准确识图理清图中各角度之间的关系也很重要．