
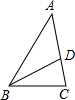 填写下列解题过程中的推理根据:
填写下列解题过程中的推理根据:

 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:初中数学 来源: 题型:
 25、填写下列解题过程中的推理根据:
25、填写下列解题过程中的推理根据:查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 | 4 |

查看答案和解析>>
科目:初中数学 来源: 题型:
已知,在平面直角坐标系xoy中,点A的坐标为(0,2),点P(m,n)是抛物线
![]() 上的一个动点.
上的一个动点.
(1)如图1,过动点P作PB⊥x轴,垂足为B,连接PA,请通过测量或计算,比较PA与PB的大小关系:PA PB(直接填写“>”“<”或“=”,不需解题过程);
(2)请利用(1)的结论解决下列问题:
①如图2,设C的坐标为(2,5),连接PC, AP+P![]() C
C![]() 是否存在最小值?如果存在,求点P的坐标;如果不存在,简单说明理由;
是否存在最小值?如果存在,求点P的坐标;如果不存在,简单说明理由;
②如图3,过动点P和原点O作直线交抛物线于另一点D,若AP=2AD,求直线OP的解析式.
 | |||
 | |||
(第24题图1) (第24题图2) (第24题图3)
查看答案和解析>>
科目:初中数学 来源:江苏期中题 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com