
分析 (1)根据抛物线C1:y1=a(x-1)2+k1(a≠0)交x轴于点(0,0),对称轴为直线x=1,可得抛物线与x轴的另一个交点,进一步得到b1的值;
(2)由与(1)相同的方法可得bn=2n,则An-1An=bn-bn-1可求;
(3)①把M(-2,0)与点A3(b3,0),b3=6代入y3=a(x-$\frac{1}{2}$b2)2+k3交即可得到结论;
②由①的结论即可得到第n条抛物线yn的顶点坐标为[n,-(n+2)2a];
(4)由已知条件得到C10:y1=a(x-10)2+-144a(a≠0)顶点N(10,-144a),A10(22,0),求得|MA10|=24,根据已知条件列方程即可得到结论.
解答 解:(1)∵抛物线C1:y1=a(x-1)2+k1(a≠0)M(-2,0)与点A1(b1,0),对称轴为直线x=1,
∴抛物线与x轴的另一个交点为(4,0),
∴b1=4;
(2)由与(1)相同的方法可得b2=6,b3=8,b4=10,
按此规律可得bn=2n+2,
∴An-1An=bn-bn-1=2n+2-2(n-1)+2=2;
(3)①∵y3=a(x-$\frac{1}{2}$b2)2+k3交x轴于点M(-2,0)与点A3(b3,0),b3=6,
∴0=a(-2-3)2+k3,
∴k3=-25a,
∴抛物线y3的顶点坐标为(3,-25a);
∴依此类推第n条抛物线yn的顶点坐标为[n,-(n+2)2a];
故答案为:3,-25a;n,-(n+2)2a;
(4)存在,理由:∵C10:y1=a(x-10)2+-144a(a≠0)顶点N(10,-144a),A10(22,0),
∴|MA10|=24,
∵△MNA10是等腰直角三角形,
∴|-144a|=$\frac{1}{2}×$24,
∴a=±$\frac{1}{12}$,
∴a=±$\frac{1}{12}$,△MNA10是等腰直角三角形.
点评 考查了二次函数综合题,主要利用了二次函数的对称性,以及顶点坐标,等腰直角三角形的性质,找到规律是解题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
| A. | a=0,b=4 | B. | a=-10,b=-4 | C. | a=10,b=-4 | D. | a=-10,b=4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 下面是小东的探究学习过程,请补充完整:
下面是小东的探究学习过程,请补充完整:| x | … | -3 | -2 | -1 | -$\frac{1}{2}$ | 0 | $\frac{1}{5}$ | $\frac{1}{2}$ | $\frac{4}{5}$ | … |
| y | … | -$\frac{1}{8}$ | $\frac{1}{3}$ | $\frac{3}{4}$ | $\frac{11}{12}$ | 1 | $\frac{39}{40}$ | m | -$\frac{3}{5}$ | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
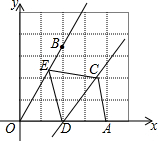 如图,在平面直角坐标系中,点A(4,0),点B(2,2$\sqrt{3}$),点C(2$\sqrt{3}$,2),点D(t,0)是线段OA上一动点,点A关于直线DC的对称点为E.若点E落在∠AOB的外部,则t的取值范围是0<t<2$\sqrt{3}$-2.
如图,在平面直角坐标系中,点A(4,0),点B(2,2$\sqrt{3}$),点C(2$\sqrt{3}$,2),点D(t,0)是线段OA上一动点,点A关于直线DC的对称点为E.若点E落在∠AOB的外部,则t的取值范围是0<t<2$\sqrt{3}$-2.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 25 | B. | 20 | C. | 0.25 | D. | 0.2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com