
 如图,港口B在港口A的正东方向,一艘船从港口A出发,沿北偏东75°方向航行20海里到C处,此时测得港口B在C的南偏东45°方向,求C到港口B的距离,(结果保留到0.01海里)(参考数据$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)
如图,港口B在港口A的正东方向,一艘船从港口A出发,沿北偏东75°方向航行20海里到C处,此时测得港口B在C的南偏东45°方向,求C到港口B的距离,(结果保留到0.01海里)(参考数据$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732) 分析 如图,作CH⊥AB于H,在AB上截取一点使得AE=EC.设CH=BH=x,则易知EC=2CH=2x,EH=$\sqrt{3}$x,在Rt△ACH中,根据AC2=CH2+AH2,可得202=x2+(2x+$\sqrt{3}$x)2,解方程即可解决问题.
解答 解:如图,作CH⊥AB于H,在AB上截取一点使得AE=EC.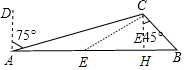
在Rt△CHB中,∵∠BCH=45°,
∴CH=BH,设CH=BH=x,
∵∠DAC=75°,∠DAB=90°,
∴∠EAC=∠ECA=15°,
∴∠CEH=∠EAC+∠ECA=30°,
∴EC=2CH=2x,EH=$\sqrt{3}$x,
在Rt△ACH中,∵AC2=CH2+AH2,
∴202=x2+(2x+$\sqrt{3}$x)2,
解得x=5$\sqrt{2}$($\sqrt{3}$-1),
∴BC=$\sqrt{2}$CH=10($\sqrt{3}$-1)=7.32海里.
答:C到港口B的距离7.32海里.
点评 本题考查解直角三角形的应用、勾股定理、直角三角形的30度角性质等知识,解题的关键是灵活运用所学知识解决问题,学会构添加常用辅助线,构建方程解决问题,属于中考常考题型.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
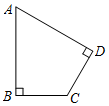 已知:如图,四边形ABCD中,∠ABC=∠ADC=90°,AB=AD.
已知:如图,四边形ABCD中,∠ABC=∠ADC=90°,AB=AD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
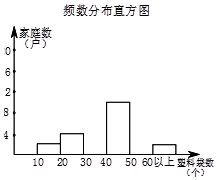 小明要统计小区500户居民每月丢弃塑料袋的数量情况,他随机调查了其中40户居民,按每月丢弃的塑料袋的数量分组进行统计,并绘制了如下的频数分布表和频数分布直方图:
小明要统计小区500户居民每月丢弃塑料袋的数量情况,他随机调查了其中40户居民,按每月丢弃的塑料袋的数量分组进行统计,并绘制了如下的频数分布表和频数分布直方图:| 组别 | 每月丢塑料袋个数 | 频数 | 频率 |
| 第1组 | 10至19 | 2 | 0.05 |
| 第2组 | 20至29 | 4 | 0.10 |
| 第3组 | 30至39 | 6 | 0.15 |
| 第4组 | 40至49 | 10 | 0.25 |
| 第5组 | 50至59 | 16 | 0.40 |
| 第6组 | 60以上 | 2 | 0.05 |
| 合计 | 40 | 1.00 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
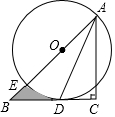 如图,在Rt△ABC中,∠C=90°,AC=BC,点O在AB上,经过点A的⊙O与BC相切于点D,交AB于点E.
如图,在Rt△ABC中,∠C=90°,AC=BC,点O在AB上,经过点A的⊙O与BC相切于点D,交AB于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com