
【题目】国庆期间,为了满足百姓的消费需求,某商店计划用170000元购进一批家电,这批家电的进价和售价如表:
类别 彩电 冰箱 洗衣机
进价(元/台) 2000 1600 1000
售价(元/台) 2300 1800 1100
若在现有资金允许的范围内,购买表中三类家电共100台,其中彩电台数是冰箱台数的2倍,设该商店购买冰箱x台.
(1)商店至多可以购买冰箱多少台?
(2)购买冰箱多少台时,能使商店销售完这批家电后获得的利润最大?最大利润为多少元?
【答案】(1)26(2)购买26台时最大利润为23000
【解析】(1)根据表格中三种家电的进价表示三种家电的总进价,小于等于170000元列出关于x的不等式,根据x为正整数,即可解答;
(2)设商店销售完这批家电后获得的利润为y元,则y=(2300-2000)2x+(1800-1600)x+(1100-1000)(100-3x)=500x+10000,结合(1)中x的取值范围,利用一次函数的性质即可解答.
(1)根据题意,得:20002x+1600x+1000(1003x)170000,
解得:x![]() ,
,
∵x为正整数,
∴x最多为26,
答:商店至多可以购买冰箱26台.
(2)设商店销售完这批家电后获得的利润为y元,
则y=(23002000)2x+(18001600)x+(11001000)(1003x)=500x+10000,
∵k=500>0,
∴y随x的增大而增大,
∵ x![]() 且x为正整数,
且x为正整数,
∴当x=26时,y有最大值,最大值为:500×26+10000=23000,
答:购买冰箱26台时,能使商店销售完这批家电后获得的利润最大,最大利润为23000元.


科目:初中数学 来源: 题型:
【题目】如图所示,将矩形纸片ABCD折叠,使点D与点B重合,点C落在点C′处,折痕为EF,若∠ABE=20°,那么∠EFC′的度数为( )

A. 115° B. 120° C. 125° D. 130°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,DE⊥AB于E,DF⊥AC于F,若BD=CD、BE=CF.
(1)求证:AD平分∠BAC;
(2)直接写出AB+AC与AE之间的等量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,
将若干个点摆成三角形图案,每条边(包括两个端点)有n(n是正整数且n>1)个点,相应的图案中总的点数记为an , 则 ![]() +
+ ![]() +…+
+…+ ![]() =( )
=( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】给出下面两个定理:
①线段垂直平分线上的点到这条线段两个端点的距离相等;
②到一条线段两个端点距离相等的点在这条线段的垂直平分线上.
应用上述定理进行如下推理:
如图,直线l是线段MN的垂直平分线.

∵点A在直线l上,∴AM=AN.( )
∵BM=BN,∴点B在直线l上.( )
∵CM≠CN,∴点C不在直线l上.
这是∵如果点C在直线l上,那么CM=CN, ( )
这与条件CM≠CN矛盾.
以上推理中各括号内应注明的理由依次是 ( )
A. ②①① B. ②①②
C. ①②② D. ①②①
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l:y=x﹣ ![]() 与x轴正半轴、y轴负半轴分别相交于A、C两点,抛物线y=
与x轴正半轴、y轴负半轴分别相交于A、C两点,抛物线y= ![]() x2+bx+c经过点B(﹣1,0)和点C.
x2+bx+c经过点B(﹣1,0)和点C.
(1)填空:直接写出抛物线的解析式:;
(2)已知点Q是抛物线y= ![]() x2+bx+c在第四象限内的一个动点.
x2+bx+c在第四象限内的一个动点.
①如图,连接AQ、CQ,设点Q的横坐标为t,△AQC的面积为S,求S与t的函数关系式,并求出S的最大值;
②连接BQ交AC于点D,连接BC,以BD为直径作⊙I,分别交BC、AB于点E、F,连接EF,求线段EF的最小值,并直接写出此时Q点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,BC=4,以顶点A,B为圆心,以AD、BC长为半径作两条弧,两弧相切于点E,且E在AB上,以AB为直径作半圆恰好与DC相切,则图中阴影部分的面积为 . 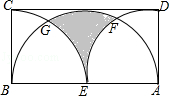
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com