
【题目】如图,已知抛物线l1:y=![]() (x﹣2)2﹣2与x轴分别交于O、A两点,将抛物线l1向上平移得到l2 , 过点A作AB⊥x轴交抛物线l2于点B,如果由抛物线l1、l2、直线AB及y轴所围成的阴影部分的面积为16,则抛物线l2的函数表达式为( )
(x﹣2)2﹣2与x轴分别交于O、A两点,将抛物线l1向上平移得到l2 , 过点A作AB⊥x轴交抛物线l2于点B,如果由抛物线l1、l2、直线AB及y轴所围成的阴影部分的面积为16,则抛物线l2的函数表达式为( )
A.y=![]() (x﹣2)2+4
(x﹣2)2+4
B.y=![]() (x﹣2)2+3
(x﹣2)2+3
C.y=![]() (x﹣2)2+2
(x﹣2)2+2
D.y=![]() (x﹣2)2+1
(x﹣2)2+1
 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:初中数学 来源: 题型:
【题目】已知:如图,在ABCD中,点F在AB的延长线上,且BF=AB,连接FD,交BC于点E.
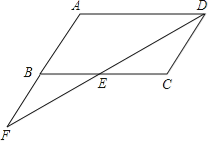
(1)说明△DCE≌△FBE的理由;
(2)若EC=3,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,E,F分别为AD,BC边上的一点,增加下列条件,不能得出BE∥DF的是( )
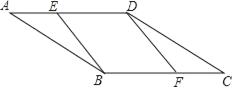
A. AE=CF B. BE=DF C. ∠EBF=∠FDE D. ∠BED=∠BFD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,E为BC边上的点(不与B,C重合),F为CD边上的点(不与C,D重合),且AE=AF,AB=4,设△AEF的面积为y,EC的长为x,求y关于x的函数关系式,并写出自变量x的取值范围.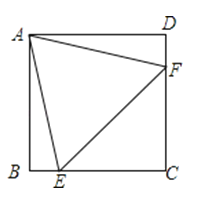
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】函数 y=![]() (a为常数)的图象上有三点(﹣4,y1),(﹣1,y2),(2,y3),则函数值y1 , y2 , y3的大小关系是( )
(a为常数)的图象上有三点(﹣4,y1),(﹣1,y2),(2,y3),则函数值y1 , y2 , y3的大小关系是( )
A.y3<y1<y2
B.y3<y2<y1
C.y1<y2<y3
D.y2<y3<y1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是面积为1的等边三角形。取BC边中点E,作ED∥AB,
EF∥AC,得到四边形EDAF,它的面积记做S1;取BE中点G,做GH∥FB,GK∥EF,
得到四边形GHFK,它的面积记作S2.照此规律作下去,
则S2018=__________________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】第五届中国机器人峰会将于5月9日在余姚开幕,某公司购买一种T恤衫参加此次峰会.了解到某商店正好有这种T恤衫的促销,当购买10件时每件140元,购买数量每增加1件单价减少1元;当购买数量为60件(含60件)以上时,一律每件80元.
(1)如果购买![]() 件(10<
件(10<![]() <60),每件的单价为
<60),每件的单价为![]() 元,请写出
元,请写出![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)如果该公司共购买了100件T恤衫,由于某种原因需分两批购买,且第一批购买量多于30件且少于60件.已知购买两批T恤衫一共花了9200元,求第一批T恤衫的购买数量.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形纸片ABCD中,对角线AC、BD交于点O,折叠正方形纸片ABCD,使AD落在BD上,点A恰好与BD上的点F重合.展开后,折痕DE分别交AB、AC于点E、G.连接GF.下列结论:①∠AGD=112.5°;②AD:AE=2;③S△AGD=S△OGD;④四边形AEFG是菱形;⑤BE=2 OG。其中正确结论的序号是______.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com