练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    16．使$\sqrt{3x-1}$有意义的x的取值范围是（　　）
    A．x＞-$\frac{1}{3}$B．x＞$\frac{1}{3}$C．x≥$\frac{1}{3}$D．x≥-$\frac{1}{3}$

    分析 根据二次根式有意义的条件列出不等式，解不等式即可．

    解答 解：由题意得，3x-1≥0，
    解得，x≥$\frac{1}{3}$，
    故选：C．

    点评 本题考查的是二次根式有意义的条件，掌握二次根式中的被开方数是非负数是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    6．某校九年级（1）班全体学生2016年初中毕业体育考试的成绩统计如表：
    成绩（分）15192224252830
    人数（人）2566876
    根据表中的信息判断，下列结论中错误的是（　　）
    A．该班一共有40名同学
    B．该班学生这次考试成绩的众数是25分
    C．该班学生这次考试成绩的中位数是25分
    D．该班学生这次考试成绩的平均数是25分

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    7．以下四个命题中真命题是（　　）
    ①三角形有且只有一个内切圆；
    ②四边形的内角和与外角和相等；
    ③顺次连接四边形各边中点所得的四边形一定是菱形；
    ④一组对边平行且一组对角相等的四边形是平行四边形．
    A．①②B．③④C．①②④D．②③④

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．在等边三角形ABC中，点E在直线AB上，点D在射线CB上，且CE=DE．

    （1）特殊情况，探索结论
    如图1，当点E是AB中点时，确定线段AE与BD的大小关系，请你直接写出结论：AE=BD（填“＞”、“＜”或“=”）．
    （2）特例启发，问题探究
    如图2，当点E是线段AB上除端点和中点外的任一点时，此时，（1）中的结论是否发生变化？写出你的猜想并加以证明．
    （3）拓展延伸
    如图3，当点E在BA的延长线上时，点D在BC边上，且CE=DE，（1）中的结论是否发生变化？写出你的猜想并加以证明．

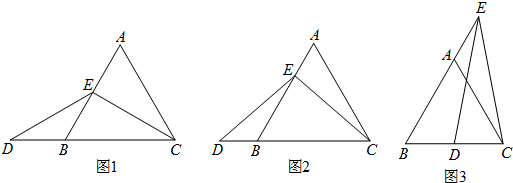
    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    11．小王参加某企业招聘测试，他的笔试、面试、技能操作得分分别为80分、85分、90分，若依次按照2：3：5的比例确定成绩，则小王的成绩是（　　）
    A．255分B．84.5分C．85.5分D．86.5分

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．【数学思考】
    如图1，A、B两地在一条河的两岸，现要在河上造一座桥MN．桥造在何处才能使从A到B的路径AMNB最短？（假定河的两岸是平行的直线，桥要与河垂直）

    【问题解决】
    如图2，过点B作BB′⊥l2，且BB′等于河宽，连接AB′交l1于点M，作MN⊥l1交l2于点N，则MN就为桥所在的位置．
    【类比联想】
    （1）如图3，正方形ABCD中，点E、F、G分别在AB、BC、CD上，且AF⊥GE，求证：AF=EG．
    （2）如图4，矩形ABCD中，AB=2，BC=x，点E、F、G、H分别在AB、BC、CD、AD上，且EG⊥HF，设y=$\frac{HF}{EG}$，试求y与x的函数关系式．
    【拓展延伸】
    如图5，一架长5米的梯子斜靠在竖直的墙面OE上，初始位置时OA=4米，由于地面OF较光滑，梯子的顶端A下滑至点C时，梯子的底端B左滑至点D，设此时AC=a米，BD=b米．
    （3）当a=1 米时，a=b．
    （4）当a在什么范围内时，a＜b？请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．已知两个二次函数y1=x2+bx+c和y2=x2+m．对于函数y1，当x=2时，该函数取最小值．
    （1）求b的值；
    （2）若函数y1的图象与坐标轴只有2个不同的公共点，求这两个公共点间的距离；
    （3）若函数y1、y2的图象都经过点（1，-2），过点（0，a-3）（a为实数）作x轴的平行线，与函数y1、y2的图象共有4个不同的交点，这4个交点的横坐标分别是x1、x2、x3、x4，且x1＜x2＜x3＜x4，求x4-x3+x2-x1的最大值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

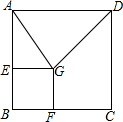    17．如图，正方形ABCD的边长是2，点E、F分别是AB、BC边上的动点（不与点A、B、C重合），且BE=BF，EG⊥AB，FG⊥BC，EG与FG相交于点G，当△ADG为等腰三角形时，BE的长为1或2-$\sqrt{2}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    18．某种商品每天的销售利润y（元）与销售单价x（元）之间满足关系：y=ax2+bx-75，其图象如图所示．
    （1）求a，b的值．
    （2）销售单价为多少元时，该种商品每天的销售利润最大？最大利润为多少元？
    （3）销售单价在什么范围时，该种商品每天的销售利润不低于21元？

    查看答案和解析>>

    同步练习册答案