
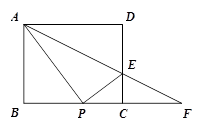
 时,求a的值.
时,求a的值.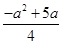 ,自变量的取值范围为:0<a<5;
,自变量的取值范围为:0<a<5;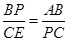 =2,再分情况讨论,从而求出a的值.
=2,再分情况讨论,从而求出a的值.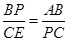 ,
,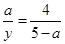 ,
,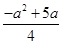 ,自变量的取值范围为:0<a<5;
,自变量的取值范围为:0<a<5;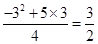 ,即CE=
,即CE=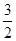 ,
,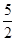 ,
,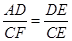 ,
,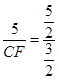 ,
,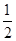 ,可得:
,可得: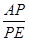 =2
=2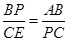 =2
=2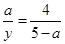 =2或
=2或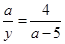 ="2"
="2" 

科目:初中数学 来源:不详 题型:解答题
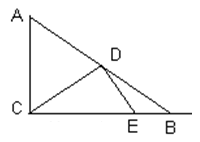
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 ,同时他测得自己的影长NH﹦336cm,而他的身长MN为168cm,求铁塔的高度.
,同时他测得自己的影长NH﹦336cm,而他的身长MN为168cm,求铁塔的高度.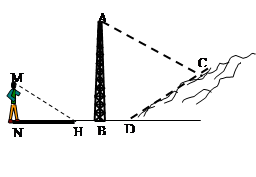
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
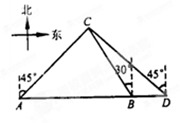
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
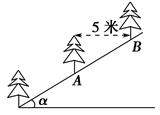
| A.5cosα | B.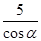 |
| C.5sinα | D.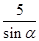 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
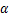 ,关于
,关于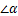 的三角函数值与梯子的倾斜程度之间,叙述正确的是( )
的三角函数值与梯子的倾斜程度之间,叙述正确的是( )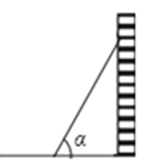
A.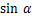 的值越大,梯子越陡 的值越大,梯子越陡 |
B.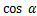 的值越大,梯子越陡 的值越大,梯子越陡 |
C. 的值越小,梯子越陡 的值越小,梯子越陡 |
D.陡缓程度与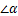 的三角函数值无关 的三角函数值无关 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com