
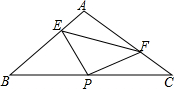
 如图Rt△ABC中,AB=AC=2,P是斜边BC中点,∠EPF两边分别交边AB、AC于E、F,且AF=BE.
如图Rt△ABC中,AB=AC=2,P是斜边BC中点,∠EPF两边分别交边AB、AC于E、F,且AF=BE.| 1 |
| 2 |
 解:(1)连接AP,
解:(1)连接AP,| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
| 2 |
|
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
| 1 |
| 2 |


科目:初中数学 来源: 题型:
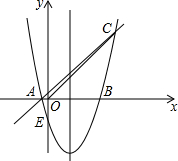 如图,对称轴为x=1的抛物线y=x2+bx+c的图象与x轴的一个交点为B(3,0),另一个交点为A,与y轴交于点E,且经过点C(4,m).
如图,对称轴为x=1的抛物线y=x2+bx+c的图象与x轴的一个交点为B(3,0),另一个交点为A,与y轴交于点E,且经过点C(4,m).| 1 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
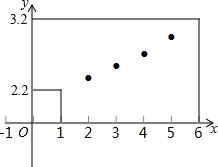 某水果种植户去年共摘得一级柑橘4000kg,并计划在今年的某个月内全部售出.由于受季节等因素影响,每千克一级柑橘的月平均售价如图所示(图中各点在同一直线上).自今年一月份开始,柑橘每多保存一个月将减少200kg,同时需要花费0.02元/kg的保存费.
某水果种植户去年共摘得一级柑橘4000kg,并计划在今年的某个月内全部售出.由于受季节等因素影响,每千克一级柑橘的月平均售价如图所示(图中各点在同一直线上).自今年一月份开始,柑橘每多保存一个月将减少200kg,同时需要花费0.02元/kg的保存费.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com