
【题目】如图,在平面直角坐标系中,矩形ABCD的顶点A、B、C的坐标分别为(0,5)(0,2)(4,2),直线l的解析式为y = kx+5-4k(k > 0).
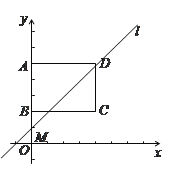
(1)当直线l经过点B时,求一次函数的解析式;
(2)通过计算说明:不论k为何值,直线l总经过点D;
(3)直线l与y轴交于点M,点N是线段DM上的一点, 且△NBD为等腰三角形,试探究:
①当函数y = kx+5-4k为正比例函数时,点N的个数有 个;
②点M在不同位置时,k的取值会相应变化,点N的个数情况可能会改变,请直接写出点N所有不同的个数情况以及相应的k的取值范围.
【答案】(1)y =![]() x+2;(2)说明见解析;(3)①2;②;当k≥2时,有3个点;当
x+2;(2)说明见解析;(3)①2;②;当k≥2时,有3个点;当![]() <k<2时,有2个点;当k=
<k<2时,有2个点;当k=![]() 时,有0个;当0<k<
时,有0个;当0<k<![]() 时,有1个.
时,有1个.
【解析】
(1)将点B坐标代入解析式求出k的值;
(2)将点D的坐标代入解析式,得出答案;
(3)根据图形的平行法则求出零界值,然后进行分类.
解: (1)将点B(0,2)代入y=kx+5-4k得![]()
∴y =![]() x+2
x+2
(2)由题意可得:点D坐标为(4,5)
把x=4代入y=kx+5-4k得y=5 ∴不论k为何值,直线l总经点D;
(3)①当函数y=kx+5-4k为正比例函数时可得5-4k=0,解得k=![]() ,
,
∴直线解析式为y=![]() x,则BM=2,如图1所示,
x,则BM=2,如图1所示,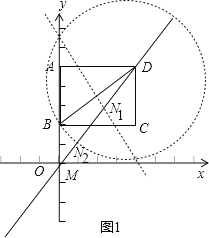
以D为圆心BD为半径画圆,与DM有一交点,BD的垂直平分线与DM有一交点,
故满足条件的点有两个.
故答案为:2;
②∵k>0,
∴5-4k<5,
当5-4k=-3时,k=2,此时OM=3,则MB=5,如图2所示,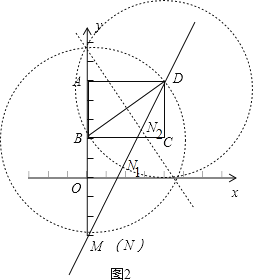
分别以B、D为圆心BD为半径画圆,与DM交于点M和N1,和BD的垂直平分线交DM于点N2,故此时满足条件的N点有3个,
当k>2时,此时MB>5,如图3所示,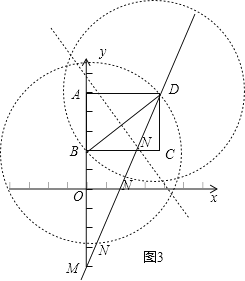
分别以B、D为圆心BD为半径画圆,与DM交于N1、N2两点,BD的垂直平分线交DM于N3,
故满足条件的点有3个,
∴当k≥2时,满足条件的点有3个,
当![]() <k<2时,此时0<OB<5,同理可得出满足条件点有两个,
<k<2时,此时0<OB<5,同理可得出满足条件点有两个,
当k=![]() 时,此时B、M重合,则满足条件的N点有0个,
时,此时B、M重合,则满足条件的N点有0个,
当0<k<![]() 时,即M在线段AB上时,同理可知满足条件的点只有一个,
时,即M在线段AB上时,同理可知满足条件的点只有一个,
综上可知当k≥2时,有3个;当![]() <k<2时,有两个;当k=
<k<2时,有两个;当k=![]() 时,有0个;当0<k<
时,有0个;当0<k<![]() 时,有1个.
时,有1个.


科目:初中数学 来源: 题型:
【题目】如图是某班甲、乙、丙三位同学最近5次数学成绩及其所在班级相应平均分的折线统计图,则下列判断错误的是( ).

A. 甲的数学成绩高于班级平均分,且成绩比较稳定
B. 乙的数学成绩在班级平均分附近波动,且比丙好
C. 丙的数学成绩低于班级平均分,但成绩逐次提高
D. 就甲、乙、丙三个人而言,乙的数学成绩最不稳
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有A,B两种商品,已知买一件A商品比买一件B商品少30元,用160元全部购买A商品的数量与用400元全部购买B商品的数量相同.
(1)A,B两种商品每件各是多少元?
(2)如果小亮准备购买A,B两种商品共10件,总费用不超过380元,且不低于300元,那么一共有几种购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,AB=4,E是BC边的中点, F是CD边上的一点, 且DF=1.若M、N分别是线段AD、AE上的动点,则MN+MF的最小值为________.
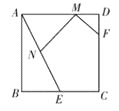
查看答案和解析>>
科目:初中数学 来源: 题型:
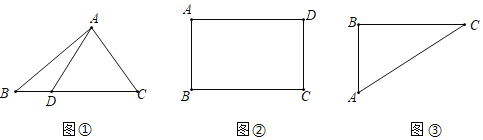
【题目】问题提出(1)如图①,在△ABC中,BC=6,D为BC上一点,AD=4,则△ABC面积的最大值是 .
问题探究(2)如图②,已知矩形ABCD的周长为12,求矩形ABCD面积的最大值.
问题解决(3)如图③,△ABC是葛叔叔家的菜地示意图,其中AB=30米,BC=40米,AC=50米,现在他想利用周边地的情况,把原来的三角形地拓展成符合条件的面积尽可能大、周长尽可能长的四边形地,用来建鱼塘.已知葛叔叔欲建的鱼塘是四边形ABCD,且满足∠ADC=60°.你认为葛叔叔的想法能否实现?若能,求出这个四边形鱼塘周长的最大值;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
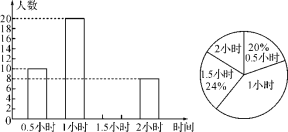
【题目】为增强学生的身体素质,教育行政部门规定学生每天参加户外活动的平均时间不少于1小时.为了解学生参加户外活动的情况,对部分学生参加户外活动的时间进行了抽样调查,并将调查结果绘制成如下两幅不完整的统计图,请你根据图中提供的信息解答下列问题:
(1)在这次调查中共调查了多少名学生?
(2)求户外活动时间为1.5小时的人数,并补全频数分布直方图;
(3)本次调查中学生参加户外活动的平均时间是否符合要求?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为了丰富学生的课余生活,计划购买排球和篮球供球类兴趣小组活动使用,若购买4个篮球和3个排球需用94元;若购买16个篮球和5个排球需用306元;
(1)求一个篮球和一个排球各多少元;
(2)该中学决定购买排球和篮球共40个,总费用不超过550元,那么该中学至少可以购买多少个排球?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 的顶点坐标为
的顶点坐标为![]() ,且与
,且与![]() 轴交于点C
轴交于点C![]() ,与
,与![]() 轴交于A、B两点(点A在点B的右侧).
轴交于A、B两点(点A在点B的右侧).
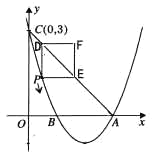
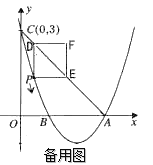
(1)求该抛物线的函数关系式;
(2)点P是该抛物线上一动点,从点C沿抛物线向点A运动(点P与A不重合),过点P作PD∥![]() 轴,交直线AC于点D;作PE∥x轴,交直线AC于点E,以PD,PE为边的矩形PEFD,问矩形PEFD周长是否存在最大值?若存在,求出此时P点的坐标及最大值;若不存在,请说明理由;
轴,交直线AC于点D;作PE∥x轴,交直线AC于点E,以PD,PE为边的矩形PEFD,问矩形PEFD周长是否存在最大值?若存在,求出此时P点的坐标及最大值;若不存在,请说明理由;
(3)在问题(2)的条件下,P点满足∠DAP=90°,且点E在![]() 轴上,点F在抛物线上,问是否存在以A、P、E、F为顶点的平行四边形?若存在,求点F的坐标;若不存在,请说明理由.
轴上,点F在抛物线上,问是否存在以A、P、E、F为顶点的平行四边形?若存在,求点F的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com