
【题目】从三角形(不是等腰三角形)一个顶点引出一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原三角形相似,我们把这条线段叫做这个三角形的完美分割线.
(1)如图,在![]() 中,CD为角平分线,
中,CD为角平分线,![]() ,
,![]() ,求证:CD为
,求证:CD为![]() 的完美分割线.
的完美分割线.

(2)如图,![]() 中,
中,![]() ,
,![]() ,CD是
,CD是![]() 的完美分割线,且
的完美分割线,且![]() 是以CD为底边的等腰三角形,求完美分割线CD的长.
是以CD为底边的等腰三角形,求完美分割线CD的长.
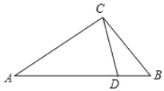
(3)在![]() 中,
中,![]() ,CD是
,CD是![]() 的完美分割线,且
的完美分割线,且![]() 为等腰三角形,直接写出∠ACB的度数.
为等腰三角形,直接写出∠ACB的度数.
【答案】(1)见解析;(2)![]() ;(3)96°或114°
;(3)96°或114°
【解析】
(1)根据完美分割线的定义只要证明①△ABC不是等腰三角形,②△ACD是等腰三角形,③△BDC∽△BCA即可;
(2)设BD=x,利用△BCD∽△BAC,列出方程即可解决问题;
(3)分三种情形讨论即可:①如图a,当AD=CD时,②如图b中,当AD=AC时,③如图c中,当AC=CD时,分别求出∠ACB即可.
(1)证明:∵∠A=40°,∠B=60°,
∴∠ACB=80°,
∴△ABC不是等腰三角形,
∵CD平分∠ACB,
∴∠ACD=∠BCD=![]() ∠ACB=40°,
∠ACB=40°,
∴∠ACD=∠A=40°,
∴△ACD为等腰三角形,
∵∠DCB=∠A=40°,∠CBD=∠ABC,
∴△BCD∽△BAC,
∴CD是△ABC的完美分割线;
(2)解:由已知AC=AD=2,
∵△BCD∽△BAC,
∴![]()
设BD=x,
∴![]() ,
,
∵x>0,
∴x=![]() ,
,
∵△BCD∽△BAC,
∴![]() ,即
,即![]() ,
,
∴CD=![]() .
.
(3)解:①当AD=CD时,如图a,
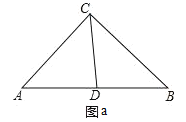
∠ACD=∠A=48°,
∵△BDC∽△BCA,
∴∠BCD=∠A=48°,
∴∠ACB=∠ACD+∠BCD=96°,
②当AD=AC时,如图b中,
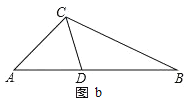
∠ACD=∠ADC=![]() =66°,
=66°,
∵△BDC∽△BCA,
∴∠BCD=∠A=48°,
∴∠ACB=∠ACD+∠BCD=114°;
③当AC=CD时,如图c中,∠ADC=∠A=48°,
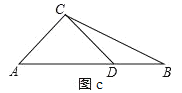
∵△BDC∽△BCA,
∴∠BCD=∠A=48°,
∵∠ADC>∠BCD,矛盾,舍弃.
综上所述,∠ACB=96°或114°;


科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC=1,∠BAC=45°,△AEF是由△ABC绕点A按顺时针方向旋转得到的.连接BE、CF相交于点D.
(1)求证:BE=CF.
(2)当四边形ACDE为菱形时,求BD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的口袋里装有分别标有汉字“美”、“丽”、“光”、“明”的四个小球,除汉字不同之外,小球没有任何区别,每次摸球前先搅拌均匀再摸球.
(1)若从中任取一个球,求摸出球上的汉字刚好是“美”的概率;
(2)甲从中任取一球,不放回,再从中任取一球,请用树状图或列表法,求甲取出的两个球上的汉字恰能组成“美丽”或“光明”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
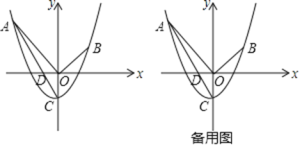
【题目】如图,在平面直角坐标系中,抛物线![]() ,过点
,过点![]() 和点
和点![]() ,与y轴交于点C,连接AC交x轴于点D,连接OA,OB
,与y轴交于点C,连接AC交x轴于点D,连接OA,OB
![]() 求抛物线
求抛物线![]() 的函数表达式;
的函数表达式;
![]() 求点D的坐标;
求点D的坐标;
![]() 的大小是______;
的大小是______;
![]() 将
将![]() 绕点O旋转,旋转后点C的对应点是点
绕点O旋转,旋转后点C的对应点是点![]() ,点D的对应点是点
,点D的对应点是点![]() ,直线
,直线![]() 与直线
与直线![]() 交于点M,在
交于点M,在![]() 旋转过程中,当点M与点
旋转过程中,当点M与点![]() 重合时,请直接写出点M到AB的距离.
重合时,请直接写出点M到AB的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
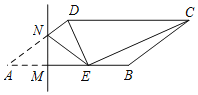
【题目】如图,已知ABCD中,AB=16,AD=10,sinA=![]() ,点M为AB边上一动点,过点M作MN⊥AB,交AD边于点N,将∠A沿直线MN翻折,点A落在线段AB上的点E处,当△CDE为直角三角形时,AM的长为_____.
,点M为AB边上一动点,过点M作MN⊥AB,交AD边于点N,将∠A沿直线MN翻折,点A落在线段AB上的点E处,当△CDE为直角三角形时,AM的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
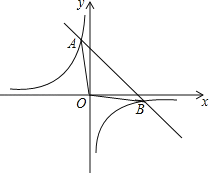
【题目】一次函数y=kx+b的图象与反比例函数![]() 的图象相交于A(﹣1,m),B(n,-1)两点.
的图象相交于A(﹣1,m),B(n,-1)两点.
(1)求出这个一次函数的表达式;
(2)求△OAB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
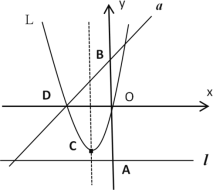
【题目】如图,若m是正数,直线l:y=-m与y轴交于点A;直线a:y=x+m与y轴交于点B;抛物线L:y= x2+mx的顶点为C,且L与x轴左交点为D.
(1)若AB=12,求m的值,此时在抛物线的对称轴上存在一点P使得△![]() 的周长最小,求点P坐标;
的周长最小,求点P坐标;
(2)当点C在直线l上方时,求点C与直线l距离的最大值;
(3)在抛物线L和直线a所围成的封闭图形的边界上,把横、纵坐标都是整数的点称为“美点”,分别直接写出m=2020和m=2020.5时“美点”的个数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】东东玩具商店用500元购进一批悠悠球,很受中小学生欢迎,悠悠球很快售完,接着又用900元购进第二批这种悠悠球,所购数量是第一批数量的1.5倍,但每套进价多了5元.
(1)求第一批悠悠球每套的进价是多少元;
(2)如果这两批悠悠球每套售价相同,且全部售完后总利润不低于25%,那么每套悠悠球的售价至少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,M、N是对角线AC上的两个动点,P是正方形四边上的任意一点,且AB=4,MN=2,设AM=x,在下列关于△PMN是等腰三角形和对应P点个数的说法中,
①当x=0(即M、A两点重合)时,P点有6个;
②当P点有8个时,x=2![]() ﹣2;
﹣2;
③当△PMN是等边三角形时,P点有4个;
④当0<x<4![]() ﹣2时,P点最多有9个.
﹣2时,P点最多有9个.
其中结论正确的是( )

A. ①② B. ①③ C. ②③ D. ③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com