
【题目】已知抛物线y=x2﹣2x﹣3.
(1)抛物线与x的交点坐标是 ,顶点是 .
(2)选取适当的数据填入下表.在直角坐标系中利用五点法画出此抛物线的图象.
X | … | … | |||||
y | … | … |
(3)结合函数图象,回答下题:
若抛物线上两点A(x1,y1),B(x2,y2)的横坐标满足x1<x2<1比较y1,y2的大小: .当y<0,自变量x的取值范围是 .
【答案】(1)(﹣1,0),(3,0);(1,4);(2)详见解析;(3)y1>y2,﹣1<x<3.
【解析】
(1)解方程x2﹣2x﹣3=0得抛物线与x轴的交点坐标,利用配方法得到y=(x﹣1)2﹣4,从而得到抛物线的顶点坐标;
(2)利用描点法画函数图象;
(3)利用二次函数的性质判断y1,y2的大小,结合函数图象写出函数图象在x轴下方所对应的自变量的范围即可.
解:(1)当y=0时,x2﹣2x﹣3=0,解得x1=﹣1,x2=3,
∴抛物线与x轴的交点坐标是(﹣1,0)(3,0);
∵y=x2﹣2x﹣3
y=x2﹣2x+1-4
y=(x﹣1)2﹣4,
∴抛物线的顶点坐标为(1,﹣4);
故答案为: (﹣1,0),(3,0);(1,4);
(2)如图,

如图,
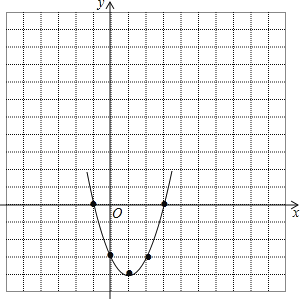
(3)由题意可知,抛物线对称轴为直线x=1,开口向上
∴当x1<x2<1时,y1>y2:
当y<0,自变量x的取值范围是﹣1<x<3.
故答案为(﹣1,0)(3,0);(1,﹣4);y1>y2:1<x<3.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:
【题目】已知:甲、乙两车分别从相距300km的A,B两地同时出发相向而行,甲到B地后立即返回,下图是它们离各自出发地的距离y与行驶时间x之间的函数图象.
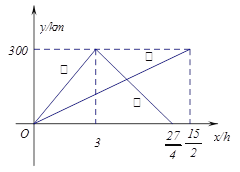
(1)求甲车离出发地的距离y与行驶时间x之间的函数关系式,并标明自变量![]() 的取值范围;
的取值范围;
(2)若已知乙车行驶的速度是40千米/小时,求出发后多长时间,两车离各自出发地的距离相等;
(3)它们在行驶过程中有几次相遇.并求出每次相遇的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
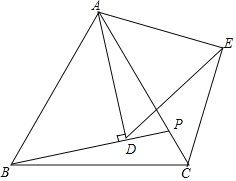
【题目】如图,△ABC为等边三角形,点P是线段AC上一动点(点P不与A,C重合),连接BP,过点A作直线BP的垂线段,垂足为点D,将线段AD绕点A逆时针旋转60°得到线段AE,连接DE,CE.
(1)求证:BD=CE;
(2)延长ED交BC于点F,求证:F为BC的中点;
(3)在(2)的条件下,若△ABC的边长为1,直接写出EF的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,抛物线![]() 与x轴交于A,B两点(A在B的左侧),与y轴交于点C,顶点为D.
与x轴交于A,B两点(A在B的左侧),与y轴交于点C,顶点为D.
(1)请直接写出点A,C,D的坐标;
(2)如图(1),在x轴上找一点E,使得△CDE的周长最小,求点E的坐标;
(3)如图(2),F为直线AC上的动点,在抛物线上是否存在点P,使得△AFP为等腰直角三角形?若存在,求出点P的坐标,若不存在,请说明理由.
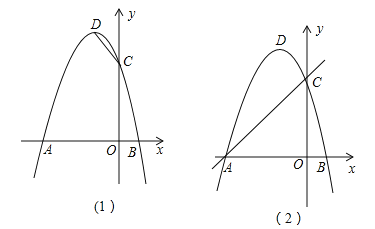
查看答案和解析>>
科目:初中数学 来源: 题型:
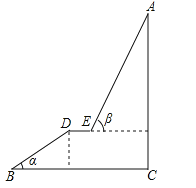
【题目】如图,A为某旅游景区的最佳观景点,游客可从B处乘坐缆车先到达小观景平台DE观景,然后再由E处继续乘坐缆车到达A处,返程时从A处乘坐升降电梯直接到达C处,已知:AC⊥BC于C,DE∥BC,BC=110米,DE=9米,BD=60米,α=32°,β=68°,求AC的高度.(参考数据:sin32°≈0.53;cos32°≈0.85;tan32°≈0.62;sin68°≈0.93;cos68°≈0.37;tan68°≈2.48)
查看答案和解析>>
科目:初中数学 来源: 题型:
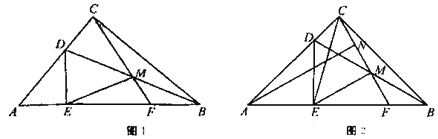
【题目】如图1,Rt△ABC中,∠ACB=90°,点D为边AC上一点,DE⊥AB于点E,点M为BD中点,CM的延长线交AB于点F.
(1)求证:CM=EM;
(2)若∠BAC=50°,求∠EMF的大小;
(3)如图2,若△DAE≌△CEM,点N为CM的中点,求证:AN∥EM.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图;![]() 三个顶点的坐标分别为
三个顶点的坐标分别为![]() ,
,![]() ,
,![]()

(1)请画出将![]() 向左平移4个单位长度后得到的图形
向左平移4个单位长度后得到的图形![]() ;
;
(2)请画出![]() 关于点
关于点![]() 成中心对称的图形
成中心对称的图形![]() ;
;
(3)若![]() 绕点
绕点![]() 旋转可以得到
旋转可以得到![]() ,请直接写出点
,请直接写出点![]() 的坐标;
的坐标;
(4)在![]() 轴上找一点
轴上找一点![]() ,使
,使![]() 的值最小,请直接写出点
的值最小,请直接写出点![]() 的坐标.
的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com