
如图,直线y=mx与双曲线y= 相交于A、B两点,A点的坐标为(1,2)
相交于A、B两点,A点的坐标为(1,2)
(1)求反比例函数的表达式;
(2)根据图象直接写出当mx> 时,x的取值范围;
时,x的取值范围;
(3)计算线段AB的长.
(1)反比例函数的表达式是y=;
(2)当mx>时,x的取值范围是﹣1<x<0或x>1;
(3)AB=2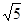 .
.
解析试题分析:(1)将点A的坐标代入反比例函数的解析式即可求出;
(2)将点A的坐标代入直线的解析式可求出直线的解析式,解y=mx与y= 组成的方程组求出B的坐标,根据A、B的坐标结合图象就可以得出;
组成的方程组求出B的坐标,根据A、B的坐标结合图象就可以得出;
(3)利用勾股定理分别求出OA、OB,即可得出.
试题解析:(1)把A(1,2)代入y= 得:k=2,
得:k=2,
即反比例函数的表达式是y= ;
;
(2)把A(1,2)代入y=mx得:m=2,
即直线的解析式是y=2x,
解方程组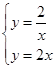 得出B点的坐标是(﹣1,﹣2),
得出B点的坐标是(﹣1,﹣2),
∴当mx> 时,x的取值范围是﹣1<x<0或x>1;
时,x的取值范围是﹣1<x<0或x>1;
(3)过A作AC⊥x轴于C,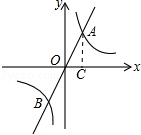
∵A(1,2),
∴AC=2,OC=1,
由勾股定理得:AO=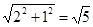 ,
,
同理求出OB=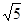 ,
,
∴AB=2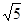 .
.
考点:1、反比例函数;2、一次函数;3、方程组的解;4、勾股定理


 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:初中数学 来源: 题型:解答题
甲、乙两人从顺义少年宫出发,沿相同的线路跑向顺义公园,甲先跑一段路程后,乙开始出发,当乙超过甲150米时,乙停在此地等候甲,两人相遇后,乙和甲一起以甲原来的速度跑向顺义公园,如图是甲、乙两人在跑步的全过程中经过的路程y(米)与甲出发的时间x(秒)的函数图象,请根据题意解答下列问题.
(1)在跑步的全过程中,甲共跑了 米,甲的速度为 米/秒;
(2)求乙跑步的速度及乙在途中等候甲的时间;
(3)求乙出发多长时间第一次与甲相遇?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
为了考察冰川融化的状况,一支科考队在某冰川上设一定一个以大本营O为圆心,半径为4km 圆形考察区域,线段P1、P2是冰川的部分边界线(不考虑其它边界),当冰川融化时,边界线沿着与其垂直的方向朝考察区域平行移动.若经过n年,冰川的边界线P1P2移动的距离为s(km),并且s与n(n为正整数)的关系是 .以O为原点,建立如图所示的平面直角坐标系,其中P1、P2的坐标分别是(–4,9)、(–13,–3).
.以O为原点,建立如图所示的平面直角坐标系,其中P1、P2的坐标分别是(–4,9)、(–13,–3).
(1)求线段P1P2所在的直线对应的函数关系式;
(2)求冰川的边界线移动到考察区域所需要的最短时间.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
已知两直线L1:y=k1x+b1,L2:y=k2x+b2,若L1⊥L2,则有k1•k2=﹣1.
(1)应用:已知y=2x+1与y=kx﹣1垂直,求k;
(2)直线经过A(2,3),且与y= x+3垂直,求解析式.
x+3垂直,求解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
在“母亲节”到来之际,某校九年级团支部组织全体团员到敬老院慰问.为筹集慰问金,团员们利用课余期间去卖鲜花.已知团员们从花店按每 支1.5元的价格买进鲜花共 支,并按每支5元的价格全部卖出,若从花店购买鲜花的同时,还用去50元购买包装材料.
支,并按每支5元的价格全部卖出,若从花店购买鲜花的同时,还用去50元购买包装材料.
(1)求所筹集的慰问金y(元)与x(支)之间的函数表达式;
(2)若要筹集不少于650元的慰问金,则至少要卖出鲜花多少支?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
反比例函数 在第二象限的图象如图所示.
在第二象限的图象如图所示.
(1)直接写出m的取值范围;
(2)若一次函数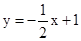 的图象与上述反比例函数图象交于点A,与x轴交于点B,△AOB的面积为
的图象与上述反比例函数图象交于点A,与x轴交于点B,△AOB的面积为 ,求m的值.
,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,已知等腰△AOB放置在平面直角坐标系xOy中, OA=OB,点B的坐标为(3,4) .
(1)求直线AB的解析式;
(2)问将等腰△AOB沿x轴正方向平移多少个单位,能使点B落在反比例函数 (x>0)的图象上.
(x>0)的图象上.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com