如图，在平面直角坐标系xOy中，矩形ABCD的边AD=6，A（1，0）， B（9，0），直线y=kx+b经过B、D两点．
（1）求直线y=kx+b的表达式；
（2）将直线y=kx+b平移，当它与矩形没有公共点时，直接写出b的取值范围．
第1卷单元月考期中期末系列答案科目：初中数学 来源： 题型：解答题
在一条笔直的公路旁依次有A、B、C三个村庄，甲、乙两人同时分别从A、B两村出发，甲骑摩托车，乙骑电动车沿公路匀速驶向C村，最终到达C村．设甲、乙两人到C村的距离y1，y2（km）与行驶时间x（h）之间的函数关系如图所示，请回答下列问题：
（1）A、C两村间的距离为 km，a= ；
（2）求出图中点P的坐标，并解释该点坐标所表示的实际意义；
（3）乙在行驶过程中，何时距甲10km？
查看答案和解析>>
科目：初中数学 来源： 题型：解答题
已知A、B两地相距300千米，甲、乙两车同时从A地出发，以各自的速度匀速往返两地，甲车先到达B地，停留1小时后按原路返回．设两车行驶的时间为x小时，离开A地的距离是y千米，如图是y与x的函数图象．
(1)计算甲车的速度为 千米／时，乙车的速度为 千米／时；
(2)几小时后两车相遇；
(3)在从开始出发到两车相遇的过程中，设两车之间的距离为S千米，乙车行驶的时间为t小时，求S与t之间的函数关系式．
查看答案和解析>>
科目：初中数学 来源： 题型：解答题
设
，
是任意两个不等实数，我们规定：满足不等式≤
≤
的实数的所有取值的全体叫做闭区间，表示为
. 对于一个函数，如果它的自变量与函数值
满足：当m≤≤n时，有m≤≤n，我们就称此函数是闭区间
上的“闭函数”.
（1）反比例函数
是闭区间
上的“闭函数”吗？请判断并说明理由；
（2）若一次函数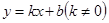
是闭区间上的“闭函数”，求此函数的表达式；
（3）若二次函数
是闭区间上的“闭函数”，直接写出实数， 的值.
查看答案和解析>>
科目：初中数学 来源： 题型：解答题
在学习三角形中线的知识时，小明了解到：三角形的任意一条中线所在的直线可以把该三角形分为面积相等的两部分。进而，小明继续研究，过四边形的某一顶点的直线能否将该四边形平分为面积相等的两部分？他画出了如下示意图（如图1），得到了符合要求的直线AF.
小明的作图步骤如下：
第一步：连结AC；
第二步：过点B作BE//AC交DC的延长线于点E；
第三步：取ED中点F，作直线AF；
则直线AF即为所求.
请参考小明思考问题的方法，解决问题：
如图2，五边形ABOCD，各顶点坐标为：A(3,4)，B(0,2)，O(0,0)，C(4,0)，D(4,2).请你构造一条经过顶点A的直线，将五边形ABOCD分为面积相等的两部分，并求出该直线的解析式.
查看答案和解析>>
科目：初中数学 来源： 题型：解答题
如图，一次函数y＝kx＋3的图象分别交x轴、y轴于点C、点D，与反比例函数
的图象在第四象限相交于点P，并且PA⊥x轴于点A，PB⊥y轴于点B，已知B（0，－6）且S△DBP＝27.
（1）求上述一次函数与反比例函数的表达式；
（2）设点Q是一次函数y＝kx＋3图象上的一点，且满足△DOQ的面积是△COD面积的2倍，直接写出点Q的坐标.
（3）若反比例函数
的图象与△ABP总有公共点，直接写出n的取值范围.
查看答案和解析>>
科目：初中数学 来源： 题型：解答题
已知一次函数
的图象经过点（
，
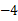），且与正比例函数
的图象相交于点（4，
），
求：（1）的值；
（2）
、
的值；
（3）求出这两个函数的图象与
轴相交得到的三角形的面积．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
；（2）
或
.
，当它左移超过点A或右移超过点C时，它与矩形没有公共点 .因此，只要将A， C两点坐标分别代入
的值即可求得b的取值范围
，解得 
.
经过点(1，－1)，求关于x的不等式2x－b≥0的解集.