
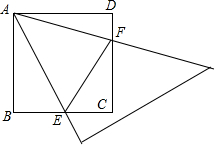
 如图,将一把含45°角的三角尺,放在正方形ABCD上,三角尺绕着顶点A转动时,与正方形的BC、CD两边分别交于点E、F.
如图,将一把含45°角的三角尺,放在正方形ABCD上,三角尺绕着顶点A转动时,与正方形的BC、CD两边分别交于点E、F.分析 (1)延长FD至G,使DG=BE,连接AG,先证△ABE≌△ADG,再证△GAF≌△EAF即可;
(2)在Rt△EFC中,利用勾股定理即可解决问题;
解答 解:(1)EF=BE+DF.
延长FD至G,使DG=BE,连接AG,如图①,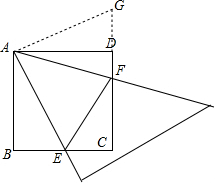
∵ABCD是正方形,
∴AB=AD,∠ABE=ADG=∠DAB=90°,
∴△ABE≌△ADG,
∴AE=AG,∠DAG=∠EAB,
∵∠EAF=45°,
∴∠DAF+∠EAB=45°,
∴∠DAF+∠DAG=45°,
∴∠GAF=∠EAF=45°,
∵AF=AF,
∴△GAF≌△EAF,
∴EF=GF,
∴GF=DF+DG=DF+BE,
即:EF=DF+BE.
(2)如图所示,已知BE=x,DF=y,则CE=1-x,CF=1-y,
由(1)可知EF=x+y,
在Rt△CEF中,由勾股定理,得
CE2+CF2=EF2,即(1-x)2+(1-y)2=(x+y)2,
解得:y=$\frac{1-x}{1+x}$(0≤x≤1).
点评 本题考查了旋转变换、正方形的性质、全等三角形判定与性质、勾股定理等知识点,难度适中.对于线段和差关系的证明,截长补短是常用手段,并且本题是经典的“大角夹半角”模型,其结论和推导过程要牢记,以便再遇到类似问题时可迅速解答.


 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:初中数学 来源: 题型:选择题
 如图,在平面直角坐标系中,已知A(1,0),D(3,0),△ABC与△DEF位似,原点O是位似中心.若AB=1.5,则DE=( )
如图,在平面直角坐标系中,已知A(1,0),D(3,0),△ABC与△DEF位似,原点O是位似中心.若AB=1.5,则DE=( )| A. | 2 | B. | 3 | C. | 4.5 | D. | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
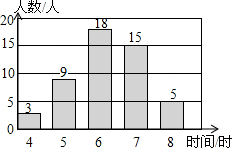 在开展“国学诵读”活动中,某校为了解全校1200名学生课外阅读的情况,随机调查了50名学生一周的课外阅读时间,并绘制成如图所示的条形统计图.根据图中数据,估计该校1200名学生一周的课外阅读时间为8小时的人数是120.
在开展“国学诵读”活动中,某校为了解全校1200名学生课外阅读的情况,随机调查了50名学生一周的课外阅读时间,并绘制成如图所示的条形统计图.根据图中数据,估计该校1200名学生一周的课外阅读时间为8小时的人数是120.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
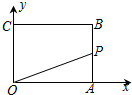 如图,已知矩形OABC,A(4,0),C(0,3),动点P从点A出发,沿A-B-C-O的路线勻速运动,设动点P的运动时间为t,△OAP的面积为S,则下列能大致反映S与t之间关系的图象是( )
如图,已知矩形OABC,A(4,0),C(0,3),动点P从点A出发,沿A-B-C-O的路线勻速运动,设动点P的运动时间为t,△OAP的面积为S,则下列能大致反映S与t之间关系的图象是( )| A. |  | B. |  | C. | 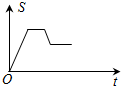 | D. | 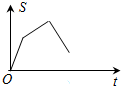 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
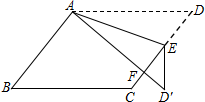 如图,在?ABCD中,E为边CD上一点,将△ADE沿AE折叠至△AD′E处,AD′与CE交于点F.若∠B=50°,∠DAE=20°,则∠FED′的大小为40度.
如图,在?ABCD中,E为边CD上一点,将△ADE沿AE折叠至△AD′E处,AD′与CE交于点F.若∠B=50°,∠DAE=20°,则∠FED′的大小为40度.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com