
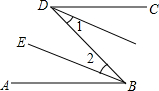
 已知:DC∥AB,DF平分∠CDB,BE平分∠ABD
已知:DC∥AB,DF平分∠CDB,BE平分∠ABD ________,∠2=
________,∠2= ________
________ ∠CDB,∠2=
∠CDB,∠2= ∠ABD,则∠1=∠2,然后根据平行线的判定即可得到BE∥DF.
∠ABD,则∠1=∠2,然后根据平行线的判定即可得到BE∥DF. ∠CDB,∠2=
∠CDB,∠2= ∠ABD (角平分线的定义),
∠ABD (角平分线的定义),

科目:初中数学 来源: 题型:
 在下面推理过程的括号内填上推理的依据
在下面推理过程的括号内填上推理的依据| ∥ | . |
查看答案和解析>>
科目:初中数学 来源: 题型:
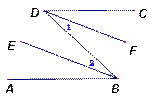
 已知:DC∥AB,DF平分∠CDB,BE平分∠ABD
已知:DC∥AB,DF平分∠CDB,BE平分∠ABD| 1 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
已知:DC∥AB DF平分∠CDB ,BE平分∠ABD
求证 BE∥DF 在空格处填角 括号内填推理的依据
证明 ∵DC∥AB(已知)
∴∠ABD=
( )
又∵DF平分∠CDB BE平分∠ABD (已知)
∴∠1=![]() ∠2=
∠2=![]() ( )
( )
∴∠1=∠2 ( )
∴BE∥DF ( )
查看答案和解析>>
科目:初中数学 来源: 题型:
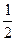 ∠2=
∠2=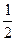 ( )
( )查看答案和解析>>
科目:初中数学 来源:2010年安庆市外国语学校八年级第一学期期中考试数学卷 题型:解答题
已知:DC∥AB DF平分∠CDB ,BE平分∠ABD
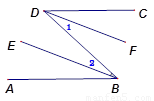
求证 BE∥DF 在空格处填角 括号内填推理的依据
证明 ∵DC∥AB(已知)
∴∠ABD=
( )
又∵DF平分∠CDB BE平分∠ABD (已知)
∴∠1=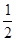 ∠2=
∠2=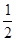 (
)
(
)
∴∠1=∠2 ( )
∴BE∥DF ( )
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com