
ЁОЬтФПЁПЃЈЬНОПЃЉЃЈ1ЃЉЙлВьЯТСаЫуЪНЃЌВЂЭъГЩЬюПеЃК
![]() ЃЛ
ЃЛ
![]() ЃЛ
ЃЛ
![]() ЃЛ
ЃЛ
![]() ЃЛ
ЃЛ
ЁЁ
![]() .ЃЈ
.ЃЈ![]() ЪЧе§ећЪ§ЃЉ
ЪЧе§ећЪ§ЃЉ
ЃЈ2ЃЉФГЪавЛЙуГЁгУе§СљБпаЮЁЂе§ЗНаЮКЭе§Ш§НЧаЮЕиАхзЉЦЬЩшЭМАИЃЌЭМАИжабыЪЧвЛПще§СљБпаЮЕиАхзЉЃЌжмЮЇЪЧе§ЗНаЮКЭе§Ш§НЧаЮЕФЕиАхзЉЃЌДгРяЯђЭтЕквЛВуАќРЈ6Пще§ЗНаЮКЭ6Пще§Ш§НЧаЮЕиАхзЉЃЛЕкЖўВуАќРЈ6Пще§ЗНаЮКЭ18Пще§Ш§НЧаЮЕиАхзЉЃЛвдДЫЕнЭЦ.
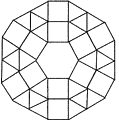
ЂйЕк3ВужаЗжБ№КЌга______Пще§ЗНаЮКЭ______Пще§Ш§НЧаЮЕиАхзЉЃЛ
ЂкЕк![]() ВужаКЌга______Пще§Ш§НЧаЮЕиАхзЉЃЈгУКЌ
ВужаКЌга______Пще§Ш§НЧаЮЕиАхзЉЃЈгУКЌ![]() ЕФДњЪ§ЪНБэЪОЃЉ.
ЕФДњЪ§ЪНБэЪОЃЉ.
ЃЈгІгУЃЉ
ИУЪаДђЫудквЛИіаТНЈЙуГЁжабыЃЌвВВЩгУетИібљЪНЕФЭМАИЦЬЩшЕиУцЃЌЯжга1Пще§СљБпаЮЁЂ150Пще§ЗНаЮКЭ420Пще§Ш§НЧаЮЕиАхзЉЃЌЮЪЃКЦЬЩшетбљЕФЭМАИЃЌзюЖрФмЦЬЖрЩйВуЃПЧыЫЕУїРэгЩ.
ЁОД№АИЁПЁОЬНОПЁП:ЃЈ1ЃЉn2ЃЛЃЈ2ЃЉЂй 6ЃЌ30ЃЛЂк 6(2nЉ1) Лђ12nЉ6ЃЛЁОгІгУЁПЃКЦЬЩшетбљЕФЭМАИЃЌзюЖрФмЦЬ8ВуЃЌМћНтЮі.
ЁОНтЮіЁП
[ЬНОП]ЃЈ1ЃЉЙлВьЫуЪНЙцТЩЃЌ1+3+5++ЃЈ2n-1ЃЉ=n2ЃЛ
ЃЈ2ЃЉЂйЕквЛВу6Пще§ЗНаЮКЭ6Пще§Ш§НЧаЮЕиАхзЉЃЌЕкЖўВу6Пще§ЗНаЮКЭ6+12=18Пще§Ш§НЧаЮЕиАхзЉЃЌЕкШ§Ву6Пще§ЗНаЮКЭ18+12=30Пще§Ш§НЧаЮЕиАхзЉЃЛ
ЂкЕквЛВу6=6ЁС1=6ЁСЃЈ2ЁС1-1ЃЉПще§Ш§НЧаЮЕиАхзЉЃЌЕкЖўВу18=6ЁС3=6ЁСЃЈ2ЁС2-1ЃЉПще§Ш§НЧаЮЕиАхзЉЃЌЕкШ§Ву30=6ЁС5=6ЁСЃЈ2ЁС3-1ЃЉПще§Ш§НЧаЮЕиАхзЉЃЌЕкnВу6=6ЁС1=6ЃЈ2n-1ЃЉПще§Ш§НЧаЮЕиАхзЉЃЌ
[гІгУ]
150Пще§ЗНаЮЕиАхзЉПЩвдЦЬЩшетбљЕФЭМАИ150ЁТ6=25ЃЈВуЃЉЃЌЦЬЩшnВуашвЊе§Ш§НЧаЮЕиАхзЉЕФЪ§СПЮЊЃК6[1+3+5++ЃЈ2n-1ЃЉ]=6n2ЃЌ6n2=420ЃЌn2=70ЃЌn=![]() ЃЌ8ЃМnЃМ9ЃЌЫљвд420Пще§Ш§НЧаЮЕиАхзЉзюЖрПЩвдЦЬЩшетбљЕФЭМАИ8ВуЃЎвђДЫЦЬЩшетбљЕФЭМАИЃЌзюЖрФмЦЬ8ВуЃЎ
ЃЌ8ЃМnЃМ9ЃЌЫљвд420Пще§Ш§НЧаЮЕиАхзЉзюЖрПЩвдЦЬЩшетбљЕФЭМАИ8ВуЃЎвђДЫЦЬЩшетбљЕФЭМАИЃЌзюЖрФмЦЬ8ВуЃЎ
[ЬНОП]
ЃЈ1ЃЉЙлВьЫуЪНЙцТЩЃЌ1+3+5++ЃЈ2n-1ЃЉ=n2ЃЌ
ЙЪД№АИЮЊn2ЃЛ
(2)ЂйЁпЕквЛВуАќРЈ6Пще§ЗНаЮКЭ6Пще§Ш§НЧаЮЕиАхзЉЃЌ
ЕкЖўВуАќРЈ6Пще§ЗНаЮКЭ6+12=18Пще§Ш§НЧаЮЕиАхзЉЃЌ
ЁрЕкШ§ВуАќРЈ6Пще§ЗНаЮКЭ18+12=30Пще§Ш§НЧаЮЕиАхзЉЃЌ
ЙЪД№АИЮЊ6ЃЌ30ЃЛ
ЂкЁпЕквЛВу6=6ЁС1=6ЁСЃЈ2ЁС1-1ЃЉПще§Ш§НЧаЮЕиАхзЉЃЌ
ЕкЖўВу18=6ЁС3=6ЁСЃЈ2ЁС2-1ЃЉПще§Ш§НЧаЮЕиАхзЉЃЌЕкШ§Ву30=6ЁС5=6ЁСЃЈ2ЁС3-1ЃЉПще§Ш§НЧаЮЕиАхзЉЃЌ
ЁрЕкnВу6=6ЁС1=6ЃЈ2n-1ЃЉПще§Ш§НЧаЮЕиАхзЉЃЌ
ЙЪД№АИЮЊ6ЃЈ2n-1ЃЉЛђ12n-6ЃЎ
[гІгУ]
ЦЬЩшетбљЕФЭМАИЃЌзюЖрФмЦЬ8ВуЃЎ
Ёп![]() ЃЌЁр150Пще§ЗНаЮЕиАхзЉПЩвдЦЬЩшетбљЕФЭМАИ25ВуЃЛ
ЃЌЁр150Пще§ЗНаЮЕиАхзЉПЩвдЦЬЩшетбљЕФЭМАИ25ВуЃЛ
ЁпЦЬЩшnВуашвЊе§Ш§НЧаЮЕиАхзЉЕФЪ§СПЮЊЃК6[1+3+5++ЃЈ2nЉ1ЃЉ]=6n2ЃЌ
Ёр6n2=420ЃЌn2=70ЃЌ![]() ЃЎ
ЃЎ
гжЁп![]() ЃЌМД
ЃЌМД![]() ЃЌ
ЃЌ
Ёр420Пще§Ш§НЧаЮЕиАхзЉзюЖрПЩвдЦЬЩшетбљЕФЭМАИ8ВуЃЎ
ЁрЦЬЩшетбљЕФЭМАИЃЌзюЖрФмЦЬ8ВуЃЎ


 53ЬьЬьСЗЯЕСаД№АИ
53ЬьЬьСЗЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
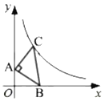
ЁОЬтФПЁПШчЭМЃЌвдЕуOЮЊдВаФЃЌABГЄЮЊжБОЖзїдВЃЌдкЁбOЩЯШЁвЛЕуCЃЌбгГЄABжСЕуDЃЌСЌНгDCЃЌЙ§ЕуAзїЁбOЕФЧаЯпНЛDCЕФбгГЄЯпгкЕуEЃЌЧвЁЯDCBЃНЁЯDAC.
(1)ЧѓжЄЃКCDЪЧЁбOЕФЧаЯпЃЛ
(2)ШєADЃН6ЃЌtanЁЯDCBЃН![]() ЃЌЧѓAEЕФГЄЃЎ
ЃЌЧѓAEЕФГЄЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊХзЮяЯпy=ax2+bx+cгыxжсНЛгкAЃЈ-1ЃЌ0ЃЉЁЂBЃЈ4ЃЌ0ЃЉСНЕуЃЌгыyжсНЛгкЕуCЃЈ0ЃЌ2ЃЉЃЌ
ЃЈ1ЃЉЧѓХзЮяЯпЕФКЏЪ§БэДяЪНЃЛ
ЃЈ2ЃЉШчЭМЃЌдкХзЮяЯпЖдГЦжсЩЯШЁСНИіЕуGЁЂHЃЈGдкHЕФЩЯЗНЃЉЃЌЧвТњзуGH=1ЃЌСЌНгCGЃЌAHЃЌЧѓЫФБпаЮCGHAЕФжмГЄЕФзюаЁжЕЃЛ
ЃЈ3ЃЉШчЭМЃЌЕуPЪЧХзЮяЯпЕквЛЯѓЯоЕФвЛИіЖЏЕуЃЌЙ§ЕуPзїPQЁЭxжсгкЕуQЃЌНЛBCгкЕуDЃЌPEЁЭBCгкЕуEЃЌЩшЁїPDEЕФУцЛ§ЮЊSЃЌЧѓЕБSШЁЕУзюДѓжЕЪБЕуPЕФзјБъЃЌВЂЧѓSЕФзюДѓжЕЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌЕу![]() ЕФзјБъЮЊ
ЕФзјБъЮЊ![]() ЃЌЕу
ЃЌЕу![]() ЪЧ
ЪЧ![]() жсе§АыжсЩЯвЛЕуЃЌвд
жсе§АыжсЩЯвЛЕуЃЌвд![]() ЮЊБпзїЕШбќжБНЧШ§НЧаЮ
ЮЊБпзїЕШбќжБНЧШ§НЧаЮ![]() ЃЌЪЙ
ЃЌЪЙ![]() ЃЌЕу
ЃЌЕу![]() дкЕквЛЯѓЯоЁЃШєЕу
дкЕквЛЯѓЯоЁЃШєЕу![]() дкКЏЪ§
дкКЏЪ§![]() ЕФЭМЯѓЩЯЃЌдђ
ЕФЭМЯѓЩЯЃЌдђ![]() ЕФУцЛ§ЮЊЃЈ ЃЉ
ЕФУцЛ§ЮЊЃЈ ЃЉ
A. ![]() .B.
.B. ![]() .C.
.C. ![]() .D.
.D. ![]() .
.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПгаСНИіКЏЪ§![]() КЭ
КЭ![]() ЃЌШєЖдгкУПИіЪЙКЏЪ§гавтвхЕФЪЕЪ§
ЃЌШєЖдгкУПИіЪЙКЏЪ§гавтвхЕФЪЕЪ§![]() ЃЌКЏЪ§
ЃЌКЏЪ§![]() ЕФжЕЮЊСНИіКЏЪ§жЕжажаНЯаЁЕФЪ§ЃЌдђГЦКЏЪ§
ЕФжЕЮЊСНИіКЏЪ§жЕжажаНЯаЁЕФЪ§ЃЌдђГЦКЏЪ§![]() ЮЊетСНИіКЏЪ§
ЮЊетСНИіКЏЪ§![]() ЁЂ
ЁЂ![]() ЕФНЯаЁжЕКЏЪ§ЁЃР§ШчЃК
ЕФНЯаЁжЕКЏЪ§ЁЃР§ШчЃК![]() ЃЌ
ЃЌ![]() ЃЌдђ
ЃЌдђ![]() ЁЂ
ЁЂ![]() ЕФНЯаЁжЕКЏЪ§
ЕФНЯаЁжЕКЏЪ§![]()
ЃЈ1ЃЉКЏЪ§![]() ЪЧКЏЪ§
ЪЧКЏЪ§![]() ЃЌ
ЃЌ![]() ЕФНЯаЁжЕКЏЪ§;
ЕФНЯаЁжЕКЏЪ§;
ЂйдкШчЭМЕФЦНУцжБНЧзјБъЯЕжаЛГіКЏЪ§![]() ЕФЭМЯё.
ЕФЭМЯё.
ЂкаДГіКЏЪ§![]() ЕФСНЬѕаджЪ.
ЕФСНЬѕаджЪ.
ЃЈ2ЃЉКЏЪ§![]() ЪЧКЏЪ§
ЪЧКЏЪ§![]() ЃЌ
ЃЌ![]() ЕФНЯаЁжЕКЏЪ§ЃЌЕБ
ЕФНЯаЁжЕКЏЪ§ЃЌЕБ![]() ЪБЃЌКЏЪ§жЕ
ЪБЃЌКЏЪ§жЕ![]() ЕФШЁжЕЗЖЮЇЮЊ
ЕФШЁжЕЗЖЮЇЮЊ![]() .ЕБ
.ЕБ![]() ШЁФГИіЗЖЮЇФкЕФШЮвтжЕЪБЃЌ
ШЁФГИіЗЖЮЇФкЕФШЮвтжЕЪБЃЌ![]() ЮЊЖЈжЕ.жБНгаДГіТњзуЬѕМўЕФ
ЮЊЖЈжЕ.жБНгаДГіТњзуЬѕМўЕФ![]() ЕФШЁжЕЗЖЮЇМАЦфЖдгІЕФ
ЕФШЁжЕЗЖЮЇМАЦфЖдгІЕФ![]() жЕ.
жЕ.
ЃЈ3ЃЉКЏЪ§![]() ЪЧКЏЪ§
ЪЧКЏЪ§![]() ЃЌ
ЃЌ![]() ЃЈ
ЃЈ![]() ЮЊГЃЪ§ЃЌЧв
ЮЊГЃЪ§ЃЌЧв![]() ЃЉЕФНЯаЁжЕКЏЪ§ЃЌЕБ
ЃЉЕФНЯаЁжЕКЏЪ§ЃЌЕБ![]() ЪБЃЌЫцзХ
ЪБЃЌЫцзХ![]() ЕФдіДѓЃЌКЏЪ§жЕ
ЕФдіДѓЃЌКЏЪ§жЕ![]() ЯШдіДѓКѓМѕаЁЃЌжБНгаДГі
ЯШдіДѓКѓМѕаЁЃЌжБНгаДГі![]() ЕФШЁжЕЗЖЮЇ.
ЕФШЁжЕЗЖЮЇ.

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
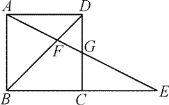
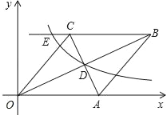
ЁОЬтФПЁПШчЭМЃЌдке§ЗНаЮABCDжаЃЌGЮЊCDБпжаЕуЃЌСЌНгAGВЂбгГЄЃЌЗжБ№НЛЖдНЧЯпBDгкЕуFЃЌНЛBCБпбгГЄЯпгкЕуEЃЎШєFGЃН2ЃЌдђAEЕФГЄЖШЮЊ( )
A. 6B. 8
C. 10D. 12
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЙигкxЕФвЛдЊЖўДЮЗНГЬx2Ѓ(mЃЋ1)xЃЋ![]() (m2ЃЋ1)ЃН0ЃЎ
(m2ЃЋ1)ЃН0ЃЎ
(1)ШєИУЗНГЬгаЪЕЪ§ИљЃЌЧѓmЕФжЕЃЎ
(2)ЖдгкКЏЪ§y1ЃНx2Ѓ(mЃЋ1)xЃЋ![]() (m2ЃЋ1)ЃЌЕБxЃО1ЪБЃЌy1ЫцзХxЕФдіДѓЖјдіДѓЃЎ
(m2ЃЋ1)ЃЌЕБxЃО1ЪБЃЌy1ЫцзХxЕФдіДѓЖјдіДѓЃЎ
ЂйЧѓmЕФЗЖЮЇЃЎ
ЂкШєКЏЪ§y2ЃН2xЃЋnгыКЏЪ§![]() НЛгкyжсЩЯЭЌвЛЕуЃЌЧѓnЕФзюаЁжЕЃЎ
НЛгкyжсЩЯЭЌвЛЕуЃЌЧѓnЕФзюаЁжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЁАВХвћГЄЩГЫЎЃЌгжЪГЮфВ§гуЁБ.вђвЛДњЮАШЫУЋдѓЖЋЕФМбОфЃЌЁАЖѕжнЮфВ§гуЁБУћбяЬьЯТ.ФГЭјЕъзЈУХЯњЪлФГжжЦЗХЦецПеАќзАЕФЮфВ§гуЪьЪГВњЦЗЃЌГЩБОЮЊ30дЊ/КаЃЌУПЬьЯњЪлy(Ка)гыЯњЪлЕЅМлx(дЊ)жЎМфДцдквЛДЮКЏЪ§ЙиЯЕЃЌШчЭМЫљЪОЃЎ
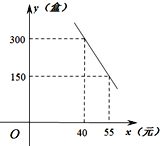
(1)ЧѓyгыxжЎМфЕФКЏЪ§ЙиЯЕЪНЃЛ
(2)ШчЙћЙцЖЈУПЬьетжжЮфВ§гуЪьЪГВњЦЗЕФЯњЪлСПВЛЕЭгк240КаЃЌЕБЯњЪлЕЅМлЮЊЖрЩйдЊЪБЃЌУПЬьЛёШЁЕФРћШѓзюДѓЃЌзюДѓРћШѓЪЧЖрЩйЃП
(3)ИУЭјЕъЕъжїШШаФЙЋвцЪТвЕЃЌОіЖЈДгУПЬьЕФЯњЪлРћШѓжаОшГі150дЊИјЯЃЭћЙЄГЬЃЌЮЊСЫБЃжЄОшПюКѓУПЬьЪЃгрРћШѓВЛЕЭгк3 600дЊЃЌЪдШЗЖЈетжжЮфВ§гуЪьЪГВњЦЗЯњЪлЕЅМлЕФЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкжБНЧзјБъЯЕжагаСтаЮOABCЃЌAЕуЕФзјБъЮЊЃЈ10ЃЌ0ЃЉЃЌЖдНЧЯпOBЁЂACЯрНЛгкЕуDЃЌЫЋЧњЯпyЃН![]() ЃЈxЃО0ЃЉОЙ§ЕуDЃЌНЛBCЕФбгГЄЯпгкЕуEЃЌЧвOBACЃН160ЃЌдђЕуEЕФзјБъЮЊ_____ЃЎ
ЃЈxЃО0ЃЉОЙ§ЕуDЃЌНЛBCЕФбгГЄЯпгкЕуEЃЌЧвOBACЃН160ЃЌдђЕуEЕФзјБъЮЊ_____ЃЎ
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com