
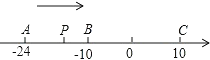
”¾ĢāÄæ”æŅŃÖŖŹżÖįÉĻÓŠA£¬B£¬CČżøöµć£¬·Ö±š±ķŹ¾ÓŠĄķŹż©24£¬©10£¬10£¬¶ÆµćP“ÓA³ö·¢£¬ŅŌĆæĆė1øöµ„Ī»µÄĖŁ¶ČĻņÖÕµćCŅĘ¶Æ£¬ÉčŅĘ¶ÆŹ±¼äĪŖtĆė£®
£Ø1£©ÓĆŗ¬tµÄ“śŹżŹ½±ķŹ¾Pµ½µćAŗĶµćCµÄ¾ąĄė£ŗ
PA=________£¬PC=________£»
£Ø2£©µ±µćPŌĖ¶Æµ½BµćŹ±£¬µćQ“ÓAµć³ö·¢£¬ŅŌĆæĆė3øöµ„Ī»µÄĖŁ¶ČĻņCµćŌĖ¶Æ£¬Qµćµ½“ļCµćŗó£¬ŌŁĮ¢¼“ŅŌĶ¬ŃłµÄĖŁ¶Č·µ»Ų£¬ŌĖ¶Æµ½ÖÕµćA£®ŌŚµćQæŖŹ¼ŌĖ¶Æŗó£¬P£¬QĮ½µćÖ®¼äµÄ¾ąĄėÄÜ·ńĪŖ2øöµ„Ī»£æČē¹ūÄÜ£¬ĒėĒó³ö“ĖŹ±µćP±ķŹ¾µÄŹż£»Čē¹ū²»ÄÜ£¬ĒėĖµĆ÷ĄķÓÉ£®
”¾“š°ø”æ£Ø1£©t£»34©t£»£Ø2£©µćP±ķŹ¾µÄŹżĪŖ©4£¬©2£¬3£¬4 .
”¾½āĪö”æ
ŹŌĢā£Ø1£©øł¾ŻPµćĪ»ÖĆ½ų¶ųµĆ³öPA£¬PCµÄ¾ąĄė£»
£Ø2£©·Ö±šøł¾ŻPµćÓėQµćĻąÓöĒ°ŅŌ¼°ĻąÓöŗó½ųŠŠĢÖĀŪ£¬½ų¶ų·Ö±š·ÖĪöµĆ³ö¼“æÉ£®
ŹŌĢā½āĪö£ŗ£Ø1£©”߶ƵćP“ÓA³ö·¢£¬ŅŌĆæĆė1øöµ„Ī»µÄĖŁ¶ČĻņÖÕµćCŅĘ¶Æ£¬ÉčŅĘ¶ÆŹ±¼äĪŖtĆė£¬
”ąPµ½µćAµÄ¾ąĄėĪŖ£ŗPA=t£¬Pµ½µćCµÄ¾ąĄėĪŖ£ŗPC=£Ø24+10£©-t=34-t£»
¹Ź“š°øĪŖ£ŗt£¬34-t£»
£Ø2£©µ±PµćŌŚQµćÓŅ²ą£¬ĒŅQµć»¹Ć»ÓŠ×·ÉĻPµćŹ±£¬
3t+2=14+t£¬
½āµĆ£ŗt=6£¬
”ą“ĖŹ±µćP±ķŹ¾µÄŹżĪŖ©4£¬
µ±PµćŌŚQµć×ó²ą£¬ĒŅQµć×·ÉĻPµćŗó£¬Ļą¾ą2øöµ„Ī»£¬
3t©2=14+t½āµĆ£ŗt=8£¬
”ą“ĖŹ±µćP±ķŹ¾µÄŹżĪŖ©2£¬
µ±Qµćµ½“ļCµćŗ󣬵±PµćŌŚQµć×ó²ąŹ±£¬
14+t+2+3t©34=34
½āµĆ£ŗt=13£¬
”ą“ĖŹ±µćP±ķŹ¾µÄŹżĪŖ3£¬
µ±Qµćµ½“ļCµćŗ󣬵±PµćŌŚQµćÓŅ²ąŹ±£¬
14+t©2+3t©34=34
½āµĆ£ŗt=14£¬
”ą“ĖŹ±µćP±ķŹ¾µÄŹżĪŖ4£¬
×ŪÉĻĖłŹö£ŗµćP±ķŹ¾µÄŹżĪŖ©4£¬©2£¬3£¬4 .



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĪŖ½ŚŌ¼ÓĆĖ®”¢±£»¤Ė®×ŹŌ“£¬±¾ŹŠÖʶØĮĖŅ»Ģ×½ŚŌ¼ÓĆĖ®µÄ¹ÜĄķ“ėŹ©£¬ĘäÖŠ¹ę¶ØĆæŌĀÓĆĖ®Į泬¹żm£Ø¶Ö£©Ź±£¬³¬¹ż²æ·ÖĆæ¶Ö¼ÓŹÕ»·¾³±£»¤·Ń ![]() ŌŖ£®ĻĀĶ¼·“Ó³ĮĖĆæŌĀŹÕČ”µÄĖ®·Ńy£ØŌŖ£©ÓėĆæŌĀÓĆĖ®Įæx£Ø¶Ö£©Ö®¼äµÄŗÆŹż¹ŲĻµµÄĶ¼Ļó£®°“ÉĻŹö·½°ø£¬Ņ»¼Ņ¾ĘµźĖÄ”¢ĪåĮ½ŌĀÓĆĖ®Įæ¼°½É·ŃĒéæöČē±ķ£ŗ
ŌŖ£®ĻĀĶ¼·“Ó³ĮĖĆæŌĀŹÕČ”µÄĖ®·Ńy£ØŌŖ£©ÓėĆæŌĀÓĆĖ®Įæx£Ø¶Ö£©Ö®¼äµÄŗÆŹż¹ŲĻµµÄĶ¼Ļó£®°“ÉĻŹö·½°ø£¬Ņ»¼Ņ¾ĘµźĖÄ”¢ĪåĮ½ŌĀÓĆĖ®Įæ¼°½É·ŃĒéæöČē±ķ£ŗ
ŌĀ·Ż | ÓĆĖ®Įæx£Ø¶Ö£© | Ė®·Ńy£ØŌŖ£© |
ĖÄŌĀ | 35 | 59.5 |
ĪåŌĀ | 80 | 151 |

£Ø1£©Ēó³ömµÄÖµ£»
£Ø2£©Š“³öyÓėxÖ®¼äµÄŗÆŹż¹ŲĻµŹ½£¬²¢Öø³ö×Ō±äĮæxµÄȔֵ·¶Ī§£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖĖıߊĪABCDŹĒ±ß³¤ĪŖ2µÄĮāŠĪ£¬”ĻBAD=60”ć£¬¶Ō½ĒĻßACÓėBD½»ÓŚµćO£¬¹żµćOµÄÖ±ĻßEF½»ADÓŚµćE£¬½»BCÓŚµćF£® 
£Ø1£©ĒóÖ¤£ŗ”÷AOE”Õ”÷COF£»
£Ø2£©Čō”ĻEOD=30”ć£¬ĒóCEµÄ³¤£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖ£¬”õABCDÖŠ”ĻABC=90”ć£¬AB=4cm£¬BC=8cm£¬ACµÄ“¹Ö±Ę½·ÖĻßEF·Ö±š½»AD”¢BCÓŚµćE”¢F£¬“¹×ćĪŖO£®
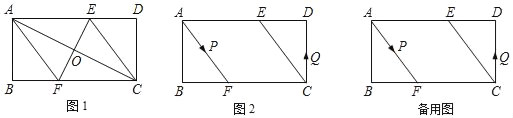
£Ø1£©ČēĶ¼1£¬Į¬½ÓAF”¢CE£®ĒóÖ¤£ŗĖıߊĪAFCEĪŖĘ½ŠŠĖıߊĪ£®
£Ø2£©ČēĶ¼1£¬ĒóAFµÄ³¤£®
£Ø3£©ČēĶ¼2£¬¶ÆµćP”¢Q·Ö±š“ÓA”¢CĮ½µćĶ¬Ź±³ö·¢£¬ŃŲ”÷AFBŗĶ”÷CDEø÷±ßŌČĖŁŌĖ¶ÆŅ»ÖÜ£®¼“µćP×ŌA”śF”śB”śAĶ£Ö¹£¬µćQ×ŌC”śD”śE”śCĶ£Ö¹£®ŌŚŌĖ¶Æ¹ż³ĢÖŠ£¬µćPµÄĖŁ¶ČĪŖĆæĆė1cm£¬µćQµÄĖŁ¶ČĪŖĆæĆė0.8cm£¬ÉčŌĖ¶ÆŹ±¼äĪŖtĆė£¬Čōµ±A”¢P”¢C”¢QĖĵćĪŖ¶„µćµÄĖıߊĪŹĒĘ½ŠŠĖıߊĪŹ±£¬ĒótµÄÖµ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
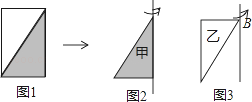
”¾ĢāÄæ”æČēĶ¼1£¬°ŃŅ»Õų¤10ĄåĆ×”¢æķ6ĄåĆ׵ij¤·½ŠĪÖ½°å·Ö³ÉĮ½øöĻąĶ¬µÄÖ±½ĒČż½ĒŠĪ£®
£Ø1£©¼×Čż½ĒŠĪ£ØČēĶ¼2£©Šż×ŖŅ»ÖÜ£¬æÉŅŌŠĪ³ÉŅ»øöŌõŃłµÄ¼øŗĪĢå£æĖüµÄĢå»żŹĒ¶ąÉŁĮ¢·½Ć×£æ
£Ø2£©ŅŅČż½ĒŠĪ£ØČēĶ¼3£©Šż×ŖŅ»ÖÜ£¬æÉŅŌŠĪ³ÉŅ»øöŌõŃłµÄ¼øŗĪĢå£æĖüµÄĢå»żŹĒ¶ąÉŁĮ¢·½Ć×£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ĢŻ×ÓŠ±ææŌŚÓėµŲĆę“¹Ö±£Ø“¹×ćĪŖO£©µÄĒ½ÉĻ£¬µ±ĢŻ×ÓĪ»ÓŚABĪ»ÖĆŹ±£¬ĖüÓėµŲĆęĖł³ÉµÄ½Ē”ĻABO=60”ć£»µ±ĢŻ×ӵ׶ĖĻņÓŅ»¬¶Æ1m£Ø¼“BD=1m£©µ½“ļCDĪ»ÖĆŹ±£¬ĖüÓėµŲĆęĖł³ÉµÄ½Ē”ĻCDO=51”ć18”䣬ĒóĢŻ×ӵij¤£® £Ø²Īæ¼Źż¾Ż£ŗsin51”ć18”ä”Ö0.780£¬cos51”ć18”ä”Ö0.625£¬tan51”ć18”ä”Ö1.248£©
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ2018ğȫ¹śĮ½»įÓŚ3ŌĀ5ČÕÖĮ20ČÕŌŚ±±¾©ÕŁæŖ£¬ĪŖĮĖĮĖ½āŹŠĆń”°»ńČ”Į½»įŠĀĪŵÄ×īÖ÷ŅŖĶ¾¾¶”±£¬¼ĒÕߊ”ĄīæŖÕ¹ĮĖŅ»“Ī³éŃłµ÷²é£¬øł¾Żµ÷²é½į¹ū»ęÖĘĮĖČēĶ¼ĖłŹ¾ÉŠ²»ĶźÕūµÄĶ³¼ĘĶ¼£®øł¾ŻĶ¼ÖŠŠÅĻ¢½ā“šĻĀĮŠĪŹĢā£ŗ
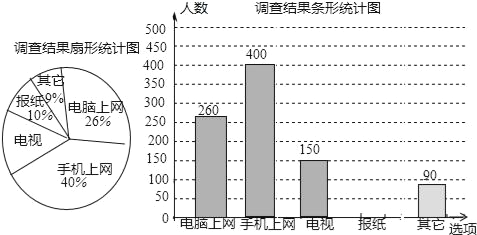
£Ø1£©Õā“Ī½ÓŹÜµ÷²éµÄŹŠĆń×ÜČĖŹżŹĒ”” ””£»
£Ø2£©ÉČŠĪĶ³¼ĘĶ¼ÖŠ£¬”°µēŹÓ”±Ėł¶ŌÓ¦µÄŌ²ŠÄ½ĒµÄ¶ČŹżŹĒ”” ””£»
£Ø3£©Ēė²¹Č«ĢõŠĪĶ³¼ĘĶ¼£»
£Ø4£©ČōøĆŹŠŌ¼ÓŠ700ĶņČĖ£¬ĒėÄć¹Ą¼ĘĘäÖŠ½«”°µēÄŌÉĻĶųŗĶŹÖ»śÉĻĶų”±×÷ĪŖ”°»ńČ”ŠĀĪŵÄ×īÖ÷ŅŖĶ¾¾¶”±µÄ×ÜČĖŹż£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĪŹĢāŅ»£ŗČēĶ¼1£¬ŅŃÖŖAC=160km£¬¼×£¬ŅŅĮ½ČĖ·Ö±š“ÓĻą¾ą30kmµÄA£¬BĮ½µŲĶ¬Ź±³ö·¢µ½CµŲ£¬Čō¼×µÄĖŁ¶ČĪŖ80km/h£¬ŅŅµÄĖŁ¶ČĪŖ60km/h£¬ÉčŅŅŠŠŹ»Ź±¼äĪŖx£Øh£©, Į½³µÖ®¼ä¾ąĄėĪŖy£Økm£©.
(1)µ±¼××·ÉĻŅŅŹ±£¬x=_________.
(2)ĒėÓĆxµÄ“śŹżŹ½±ķŹ¾y.

ĪŹĢā¶ž£ŗČēĶ¼2£¬Čō½«ÉĻŹöĻ߶ĪACĶäĒśŗóŹÓ×÷ÖÓ±ķĶāĪ§µÄŅ»²æ·Ö£¬Ļ߶ĪABÕżŗƶŌÓ¦ÖÓ±ķÉĻµÄ»”AB£Ø1Š”Ź±µÄ¼äøō£©£¬Ņ×ÖŖ”ĻAOB=30”ć.
(1)·ÖÕėODÖøĻņŌ²ÖÜÉĻµÄµćµÄĖŁ¶ČĪŖĆæ·ÖÖÓ×Ŗ¶Æ_______km£»Ź±ÕėOEÖøĻņŌ²ÖÜÉĻµÄµćµÄĖŁ¶ČĪŖĆæ·ÖÖÓ×Ŗ¶Æ_______km.
(2)Čō“Ó2:00Ęš¼ĘŹ±£¬Ēó¼ø·ÖÖÓŗó·ÖÕėÓėŹ±ÕėµŚŅ»“ĪÖŲŗĻ£æ

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅ»øöŗŠ×ÓĄļÓŠĶźČ«ĻąĶ¬µÄČżøöŠ”Ēņ£¬ĒņÉĻ·Ö±š±źÓŠŹż×Ö©2£¬1£¬4£®Ė껜ƞ³öŅ»øöŠ”Ēņ£Ø²»·Å»Ų£©£¬Ę䏿×ÖĪŖp£¬ŌŁĖ껜ƞ³öĮķŅ»øöŠ”ĒņĘ䏿×Ö¼ĒĪŖq£¬ŌņĀś×ć¹ŲÓŚxµÄ·½³Ģx2+px+q=0ÓŠŹµŹżøłµÄøÅĀŹŹĒ£Ø £©
A.![]()
B.![]()
C.![]()
D.![]()
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com