
【题目】已知⊙O的直径为10,点A,点B,点C在⊙O上,∠CAB的平分线交⊙O于点D.
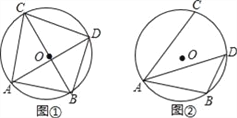
(1)如图①,若BC为⊙O的直径,AB=6,求AC,BD,CD的长;
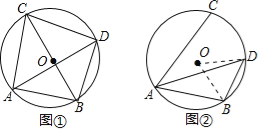
(2)如图②,若∠CAB=60°,求BD的长.
【答案】(Ⅰ)AC =8;BD=CD=5![]() ;(Ⅱ)BD=5.
;(Ⅱ)BD=5.
【解析】试题分析:(1)、根据直径得出∠CAB=∠BDC=90°,然后根据Rt△CAB的勾股定理得出AC的长度,然后根据等腰直角△BDC求出BD和CD的长度;(2)、连接OB,OD,根据AD平分∠CAB,且∠CAB=60°得出∠DOB=2∠DAB=60°,从而得出△OBD为等边三角形,从而得出BD的长度.
试题解析:(1)、如图①,∵BC是⊙O的直径,∴∠CAB=∠BDC=90°.
∵在直角△CAB中,BC=10,AB=6, ∴由勾股定理得到:AC=![]() =
=![]() =8.
=8.
∵AD平分∠CAB, ∴![]() =
=![]() ,∴CD=BD.
,∴CD=BD.
在直角△BDC中,BC=10,CD2+BD2=BC2,∴易求BD=CD=5![]() ;
;
(2)、如图②,连接OB,OD. ∵AD平分∠CAB,且∠CAB=60°,∴∠DAB=![]() ∠CAB=30°,∴∠DOB=2∠DAB=60°.
∠CAB=30°,∴∠DOB=2∠DAB=60°.
又∵OB=OD,∴△OBD是等边三角形,∴BD=OB=OD.∵⊙O的直径为10,则OB=5, ∴BD=5.


科目:初中数学 来源: 题型:
【题目】花粉的质量很小,一粒某种植物花粉的质量约为0.000037毫克,已知1克=1000毫克,那么0.000000037毫克可用科学记数法表示为( )
A.3.7×10﹣5克
B.3.7×10﹣6克
C.37×10﹣7克
D.3.7×10﹣8克
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)和正比例函数y=![]() x的图象如图所示,则方程ax2+(b﹣
x的图象如图所示,则方程ax2+(b﹣![]() )x+c=0(a≠0)的两根之和( )
)x+c=0(a≠0)的两根之和( )

A. 大于0 B. 等于0 C. 小于0 D. 不能确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列运算正确的是( )
A.﹣a(a﹣b)=﹣a2﹣ab
B.2ab3a=6a2b
C.(2ab)2÷a2b=4ab
D.(a﹣1)(1﹣a)=a2﹣1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地区为筹备一项庆典,利用现有的3490盆甲种花卉和2950盆乙种花卉搭配A,B两种园艺造型共50个摆放在迎宾大道两侧,已知搭配一个A种造型需甲种花卉80盆,乙种花卉40盆;搭配一个B种造型需甲种花卉50盆,乙种花卉90盆,且搭配一个A种造型的成本是200元,搭配一个B种造型的成本是300元,则有多少种搭配方案?这些方案中成本最低的是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com