
分析 (1)移项后两边同时除以x即可得x+$\frac{1}{x}$=3,再将其代入(x-$\frac{1}{x}$)2=(x+$\frac{1}{x}$)2-4求得代数式的值,最后开方即可;
(2)根据x+$\frac{1}{x}$=3可得x2+$\frac{1}{{x}^{2}}$=7,将其代入$\frac{{x}^{2}}{{x}^{4}-{x}^{2}+1}$=$\frac{1}{{x}^{2}-1+\frac{1}{{x}^{2}}}$即可得答案.
解答 解:(1)∵x2-3x+1=0
∴x2+1=3x,
两边同时覅除以x得:x+$\frac{1}{x}$=3,
则(x-$\frac{1}{x}$)2=(x+$\frac{1}{x}$)2-4=9-4=5,
∴x-$\frac{1}{x}$=±$\sqrt{5}$;
(2)∵x+$\frac{1}{x}$=3,
∴(x+$\frac{1}{x}$)2=9,即x2+$\frac{1}{{x}^{2}}$=7,
则$\frac{{x}^{2}}{{x}^{4}-{x}^{2}+1}$=$\frac{1}{{x}^{2}-1+\frac{1}{{x}^{2}}}$=$\frac{1}{7-1}$=$\frac{1}{6}$.
点评 本题主要考查代数式的求值能力,熟练掌握等式的基本性质和整体代入思想的应用是解题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
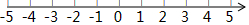 结合数轴与绝对值的知识回答下列问题:
结合数轴与绝对值的知识回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
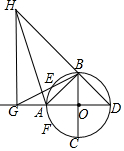 设AD、BC是圆O的互相垂直的直径,E和F分别在劣弧$\widehat{AB}$,$\widehat{CA}$上,若$\widehat{AE}$和$\widehat{AF}$相等,直线DA和直线BE的交点为G,直线FA和直线DB的交点为H,求证:∠HGA是直角.
设AD、BC是圆O的互相垂直的直径,E和F分别在劣弧$\widehat{AB}$,$\widehat{CA}$上,若$\widehat{AE}$和$\widehat{AF}$相等,直线DA和直线BE的交点为G,直线FA和直线DB的交点为H,求证:∠HGA是直角.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
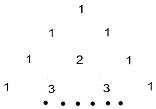 如图,为杨辉三角的一部分,它的作用是指导读者按规律写出形如(a+b)n (n为正整数)展开式的系数,请你仔细观察下列等式中的规律,利用杨辉三角解决下列问题.
如图,为杨辉三角的一部分,它的作用是指导读者按规律写出形如(a+b)n (n为正整数)展开式的系数,请你仔细观察下列等式中的规律,利用杨辉三角解决下列问题.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
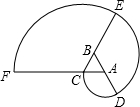 如图△ABC是正三角形,曲线CDEF叫做“正三角形的渐开线”,其中$\widehat{CD}$、$\widehat{DE}$、$\widehat{EF}$圆心依次按A、B、C…循环,它们依次相连接.若AB=1,则曲线CDEF长是4π(结果保留π).
如图△ABC是正三角形,曲线CDEF叫做“正三角形的渐开线”,其中$\widehat{CD}$、$\widehat{DE}$、$\widehat{EF}$圆心依次按A、B、C…循环,它们依次相连接.若AB=1,则曲线CDEF长是4π(结果保留π).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com