
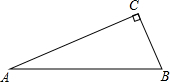
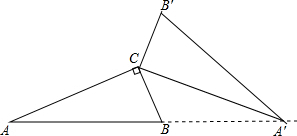
 如图,Rt△ABC中,∠C=90°,∠B=α,将△ABC绕点C逆时针旋转得到△A′B′C,当点A′落在直线AB上时,旋转角为β(其中0°<β<180°),那么β与α之间的数量关系为( )
如图,Rt△ABC中,∠C=90°,∠B=α,将△ABC绕点C逆时针旋转得到△A′B′C,当点A′落在直线AB上时,旋转角为β(其中0°<β<180°),那么β与α之间的数量关系为( )| A、β=180°-α | ||
| B、β=90°+α | ||
C、β=
| ||
| D、β=2α |


 优加精卷系列答案
优加精卷系列答案科目:初中数学 来源: 题型:
| 4 |
| 22 |
| 7 |
| 131 |
| 11 |
| 7 |
| A、3 | B、4 | C、5 | D、6 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 金额/元 | 5 | 6 | 7 | 10 |
| 人数 | 2 | 3 | 2 | 1 |
| A、6.5元 | B、6元 |
| C、3.5元 | D、7元 |
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,△ABC中,AB=13,BC=14,AC=15.点P从点B出发,以每秒2个单位的速度沿射线BC运动.设点P运动的时间为t秒,求当t为何值时,△ABP为等腰三角形?
如图,△ABC中,AB=13,BC=14,AC=15.点P从点B出发,以每秒2个单位的速度沿射线BC运动.设点P运动的时间为t秒,求当t为何值时,△ABP为等腰三角形?查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在平面直角坐标系中,点O为坐标原点,等腰△ABC,CA=CB,点A在x轴负半轴上,点B在x轴正半轴上,点C在y轴正半轴上,AB=OC,△ABC的面积为32,点D为AC中点,过点D作x轴的平行线交y轴于点E.
如图,在平面直角坐标系中,点O为坐标原点,等腰△ABC,CA=CB,点A在x轴负半轴上,点B在x轴正半轴上,点C在y轴正半轴上,AB=OC,△ABC的面积为32,点D为AC中点,过点D作x轴的平行线交y轴于点E.查看答案和解析>>
科目:初中数学 来源: 题型:
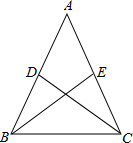 如图,在△ABC中,AB=AC,D、E分别是AB、AC上的点,要使△ABE≌△ACD,应补充条件( )
如图,在△ABC中,AB=AC,D、E分别是AB、AC上的点,要使△ABE≌△ACD,应补充条件( )| A、∠A=∠A |
| B、BE=CD |
| C、∠ABE=∠ACD |
| D、∠ABC=∠ACB. |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com