
如图,已知二次函数 的图象与
的图象与 轴相交于两个不同的点
轴相交于两个不同的点 、
、 ,与
,与 轴的交点为
轴的交点为 .设
.设 的外接圆的圆心为点
的外接圆的圆心为点 .
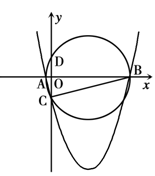
.
(1)求 与
与 轴的另一个交点D的坐标;
轴的另一个交点D的坐标;
(2)如果 恰好为
恰好为 的直径,且
的直径,且 的面积等于
的面积等于 ,求
,求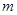 和
和 的值.
的值.
(1)(0,1);(2)

解析试题分析:(1)令x=0,代入抛物线解析式,即求得点C的坐标.由求根公式求得点A、B的横坐标,得到点A、B的横坐标的和与积,由相交弦定理求得OD的值,从而得到点D的坐标.
(2)当AB又恰好为⊙P的直径,由垂径定理知,点C与点D关于x轴对称,故得到点C的坐标及k的值.根据一元二次方程的根与系数的关系式表示出AB线段的长,由三角形的面积公式表示出△ABC的面积,可求得m的值.
(1)易求得点 的坐标为
的坐标为
由题设可知 是方程
是方程 即
即 的两根,
的两根,
所以 ,
,
所
∵⊙P与 轴的另一个交点为D,由于AB、CD是⊙P的两条相交弦,设它们的交点为点O,连结DB,
轴的另一个交点为D,由于AB、CD是⊙P的两条相交弦,设它们的交点为点O,连结DB,
∴△AOC∽△DOC,则
由题意知点 在
在 轴的负半轴上,从而点D在
轴的负半轴上,从而点D在 轴的正半轴上,
轴的正半轴上,
所以点D的坐标为(0,1);
(2)因为AB⊥CD, AB又恰好为⊙P的直径,则C、D关于点O对称,
所以点 的坐标为
的坐标为 ,即
,即
又 ,
,
所以 解得
解得
考点:一元二次方程的求根公式,根与系数的关系,相交弦定理,垂径定理,三角形的面积公式
点评:本题知识点较多,综合性强,难度较大,是中考常见题,如何表示OD及AB的长是本题中解题的关键.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:初中数学 来源: 题型:
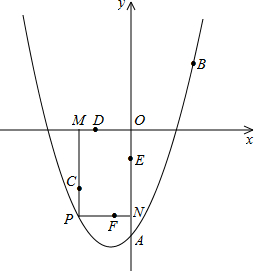
 的一个动点,过点P作x轴的垂线,垂足为D(m,0),并与直线OA交于点C.
的一个动点,过点P作x轴的垂线,垂足为D(m,0),并与直线OA交于点C.查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•呼和浩特)如图,已知二次函数的图象经过点A(6,0)、B(-2,0)和点C(0,-8).
(2013•呼和浩特)如图,已知二次函数的图象经过点A(6,0)、B(-2,0)和点C(0,-8).| 6 |
| 7 |
| 6 |
| 7 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•常德)如图,已知二次函数的图象过点A(0,-3),B(
(2013•常德)如图,已知二次函数的图象过点A(0,-3),B(| 3 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,已知二次函数的图象与x轴交于A(2,0)、B(6,0)两点,与y轴交于点D(0,4).
如图,已知二次函数的图象与x轴交于A(2,0)、B(6,0)两点,与y轴交于点D(0,4).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com