
°æƒø°ø‘ƒ∂¡¿ÌΩ‚£∫º∫÷™£∫∂‘”⁄ µ ˝a°ð0£¨b°ð0£¨¬˙◊„a+b°ð2![]() £¨µ±«“Ωˆµ±a = b ±£¨µ»∫≈≥…¡¢£¨¥À ±»°µ√¥˙ ˝ Ωa+bµƒ◊Ó–°÷µ£Æ
£¨µ±«“Ωˆµ±a = b ±£¨µ»∫≈≥…¡¢£¨¥À ±»°µ√¥˙ ˝ Ωa+bµƒ◊Ó–°÷µ£Æ
∏˘æð“‘…œΩ·¬€£¨Ω‚戓‘œ¬Œ £∫
(1)Õÿ’π£∫»Ùa>0£¨µ±«“Ωˆµ±a=___ ±£¨a+![]() ”–◊Ó–°÷µ£¨◊Ó–°÷µŒ™____£ª
”–◊Ó–°÷µ£¨◊Ó–°÷µŒ™____£ª
(2)”¶”√£∫
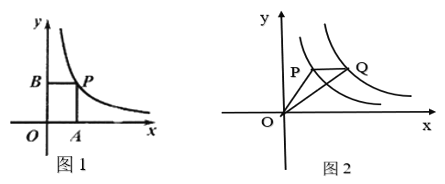
¢Ÿ»ÁÕº1£¨“—÷™µ„PŒ™À´«˙œþy=![]() (x>0)…œµƒ»Œ“‚“ªµ„£¨π˝µ„P◊˜PA°Õx÷·£¨PBÅAy÷·£¨Àƒ±þ–ŒOAPBµƒ÷Ð≥§»°µ√◊Ó–°÷µ ±£¨«Û≥ˆµ„Pµƒ◊¯±Í“‘º∞÷Ð≥§◊Ó–°÷µ£∫
(x>0)…œµƒ»Œ“‚“ªµ„£¨π˝µ„P◊˜PA°Õx÷·£¨PBÅAy÷·£¨Àƒ±þ–ŒOAPBµƒ÷Ð≥§»°µ√◊Ó–°÷µ ±£¨«Û≥ˆµ„Pµƒ◊¯±Í“‘º∞÷Ð≥§◊Ó–°÷µ£∫
¢⁄»ÁÕº2£¨“—÷™µ„Q «À´«˙œþy=![]() (x>0)…œ“ªµ„£¨«“PQ°Œx÷·£¨ ¡¨Ω”OP°¢OQ£¨µ±œþ∂ŒOP»°µ√◊Ó–°÷µ ±£¨‘⁄∆Ω√ʃ⁄»°“ªµ„C£¨ πµ√“‘0°¢P°¢Q°¢CŒ™∂•µ„µƒÀƒ±þ–Œ «∆Ω––Àƒ±þ–Œ£¨«Û≥ˆµ„Cµƒ◊¯±Í£Æ
(x>0)…œ“ªµ„£¨«“PQ°Œx÷·£¨ ¡¨Ω”OP°¢OQ£¨µ±œþ∂ŒOP»°µ√◊Ó–°÷µ ±£¨‘⁄∆Ω√ʃ⁄»°“ªµ„C£¨ πµ√“‘0°¢P°¢Q°¢CŒ™∂•µ„µƒÀƒ±þ–Œ «∆Ω––Àƒ±þ–Œ£¨«Û≥ˆµ„Cµƒ◊¯±Í£Æ
°æ¥∞∏°ø£®1£©1£ª2£ª£®2£©P(2£¨2)£ª÷Ð≥§◊Ó–°8£ª£®3£©£®-2£¨0£©°¢£®2£¨0£©ªÚ£®6£¨4£©£Æ
°æΩ‚Œˆ°ø
£®1£©∏˘æð“‚∏¯µƒ∂®“Â÷±Ω”¥˙»Îº∆À„º¥ø…£Æ
£®2£©¢Ÿ…Ë≥ˆ◊¯±Íµ„£¨∏˘æðµ⁄“ªŒ µ√≥ˆµƒΩ·¬€÷±Ω””¶”√£Æ
¢⁄¿˚”√¢ŸµƒÀº¬∑£¨…Ë≥ˆ◊¯±Íµ„P£¨‘Ÿ∏˘æðÕÍ»´∆Ω∑Ωπ´ Ω±‰–Œº¥ø…£¨«Û≥ˆPµ„◊¯±Í‘Ÿ«Û≥ˆQµ„£¨º¥ø…∏˘æð∆Ω––Àƒ±þ–Œ–‘÷ «Û≥ˆCµ„◊¯±Í£Æ
£®1£©∏˘æð“‚÷™a=![]() ±◊Ó–°£¨”÷°þa>0£¨°ýa=1£¨‘Úa+
±◊Ó–°£¨”÷°þa>0£¨°ýa=1£¨‘Úa+![]() =2£Æ
=2£Æ
£®2£©¢Ÿ…˵„P(x£¨![]() )£¨£®x>0£©£ª‘ÚÀƒ±þ–ŒOAPB÷Ð≥§Œ™2£®x+
)£¨£®x>0£©£ª‘ÚÀƒ±þ–ŒOAPB÷Ð≥§Œ™2£®x+![]() £©£¨
£©£¨
µ±x=![]() ±£¨x=2£¨¥À ±2£®x+
±£¨x=2£¨¥À ±2£®x+![]() £©”–◊Ó–°÷µ8£¨º¥÷Ð≥§◊Ó–°Œ™8£¨¥À ±µ„P(2£¨2)£Æ
£©”–◊Ó–°÷µ8£¨º¥÷Ð≥§◊Ó–°Œ™8£¨¥À ±µ„P(2£¨2)£Æ
¢⁄…˵„P(x£¨![]() )£¨£®x>0£©£ªOP=
)£¨£®x>0£©£ªOP=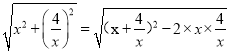 =
=![]() £¨
£¨
OP◊Ó–°£¨º¥x+![]() ◊Ó–°£¨À˘“‘x=
◊Ó–°£¨À˘“‘x=![]() £¨º¥x=2£¨°ýµ„P£®2£¨2£©£ª
£¨º¥x=2£¨°ýµ„P£®2£¨2£©£ª
”…µ„P£®2£¨2£©£¨º¥ø…÷™Qµ„◊ð◊¯±Í «2£¨¥¯»Îy=![]() (x>0)µ√µ„Q£®4£¨2£©£ª
(x>0)µ√µ„Q£®4£¨2£©£ª
À˘“‘”…O£¨P£¨Q»˝µ„◊¯±Í£¨“™ πOPQCÀƒµ„ƒÐππ≥…∆Ω––Àƒ±þ–Œ£¨‘Úµ„C◊¯±ÍŒ™£∫
£®-2£¨0£©°¢£®2£¨0£©ªÚ£®6£¨4£©£Æ


 Õ®≥«—ßµ‰ƒ¨–¥ƒÐ ÷œµ¡–¥∞∏
Õ®≥«—ßµ‰ƒ¨–¥ƒÐ ÷œµ¡–¥∞∏
| ƒÍº∂ | ∏þ÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏þ“ª | ∏þ“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ∂˛ | ∏þ∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ»˝ | ∏þ»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
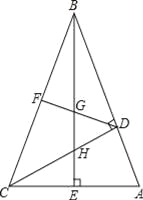
°æƒø°ø»ÁÕº£¨‘⁄°˜ABC÷–£¨°œABC=45°„£¨CD°ÕAB£¨BE°ÕAC£¨¥π◊„∑÷±Œ™D£¨E£¨FŒ™BC÷–µ„£¨BE”ÎDF£¨DC∑÷±Ωª”⁄µ„G£¨H£¨°œABE=°œCBE£Æ
£®1£©œþ∂ŒBH”ÎACœýµ»¬£ø»Ùœýµ»∏¯”Ë÷§√˜£¨»Ù≤ªœýµ»«ÎÀµ√˜¿Ì”…£ª
£®2£©«Û÷§£∫BG2©ÅGE2=EA2£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨‘⁄∆Ω√Ê÷±Ω«◊¯±Íœµ÷–£¨∞Îæ∂æ˘Œ™1∏ˆµ•Œª≥§∂»µƒ∞Α≤O1£¨O2£¨O3£¨°≠ ◊È≥…“ªÃı∆Ωª¨µƒ«˙œþ£¨µ„P¥”‘≠µ„O≥ˆ∑¢£¨—ÿ’‚Ãı«˙œþœÚ”“‘À∂Ø£¨ÀŸ∂»Œ™√ø√Î![]() ∏ˆµ•Œª≥§∂»£¨‘Úµ⁄2019√Î ±£¨µ„Pµƒ◊¯±Í «________________
∏ˆµ•Œª≥§∂»£¨‘Úµ⁄2019√Î ±£¨µ„Pµƒ◊¯±Í «________________

≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨Ω´æÿ–ŒABCDµƒÀƒ∏ˆΩ«œÚƒ⁄∑≠’€∫Û£¨«°∫√∆¥≥…“ª∏ˆŒÞ∑Ïœ∂ŒÞ÷ÿ∫œµƒÀƒ±þ–ŒEFGH£¨EH=12cm£¨EF=l6cm‘Ú±þADµƒ≥§ «£® £©
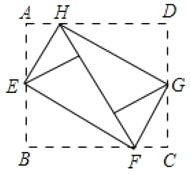
A.12cmB.16cmC.20cmD.24cm
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
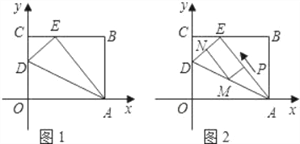
°æƒø°ø»ÁÕº1£¨OABC «“ª’≈∑≈‘⁄∆Ω√Ê÷±Ω«◊¯±Íœµ÷–µƒæÿ–Œ÷Ω∆¨£¨OŒ™‘≠µ„£¨µ„A‘⁄x÷·µƒ’˝∞Î÷·…œ£¨µ„C‘⁄y÷·µƒ’˝∞Î÷·…œ£¨OA=5£¨OC=4£Æ
£®1£©‘⁄OC±þ…œ»°“ªµ„D£¨Ω´÷Ω∆¨—ÿAD∑≠’€£¨ πµ„O¬‰‘⁄BC±þ…œµƒµ„E¥¶£¨«ÛD£¨E¡Ωµ„µƒ◊¯±Í£ª
£®2£©»ÁÕº2£¨»ÙAE…œ”–“ª∂ص„P£®≤ª”ÎA£¨E÷ÿ∫œ£©◊‘Aµ„—ÿAE∑ΩœÚEµ„‘»ÀŸ‘À∂Ø£¨‘À∂صƒÀŸ∂»Œ™√ø√Î1∏ˆµ•Œª≥§∂»£¨…Ë‘À∂صƒ ±º‰Œ™t√Σ®0£ºt£º5£©£¨π˝Pµ„◊˜EDµƒ∆Ω––œþΩªAD”⁄µ„M£¨π˝µ„M◊˜AE∆Ω––œþΩªDE”⁄µ„N£Æ«ÛÀƒ±þ–ŒPMNEµƒ√ʪ˝S”Î ±º‰t÷ƺ‰µƒ∫Ø ˝πÿœµ Ω£ªµ±t»°∫Œ÷µ ±£¨s”–◊Ó¥Û÷µ£¨◊Ó¥Û÷µ «∂ý…Ÿ£ø
£®3£©‘⁄£®2£©µƒÃıº˛œ¬£¨µ±tŒ™∫Œ÷µ ±£¨“‘A£¨M£¨EŒ™∂•µ„µƒ»˝Ω«–ŒŒ™µ»—¸»˝Ω«–Œ£¨≤¢«Û≥ˆœý”¶µƒ ±øõ„Mµƒ◊¯±Í£ø
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øŒ ±≥æ∞£∫ƒ≥ ˝—ß–À»§–°◊È∞—¡Ω∏ˆµ»—¸÷±Ω«»˝Ω«–Œµƒ÷±Ω«∂•µ„÷ÿ∫œ£¨∑¢œ÷¡À“ª–©”–»§µƒΩ·¬€£Æ
Ω·¬€“ª£∫
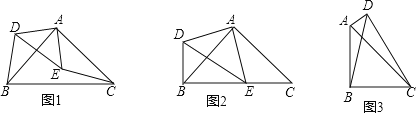
£®1£©»ÁÕº1£¨‘⁄°˜ABC°¢°˜ADE÷–£¨°œBAC£Ω°œDAE£Ω90°„£¨AB£ΩAC£¨AD£ΩAE£¨¡¨Ω”BD£¨CE£¨ ‘Àµ√˜°˜ADB°’°˜AEC£ª
Ω·¬€∂˛£∫
£®2£©»ÁÕº2£¨‘⁄£®1£©µƒÃıº˛œ¬£¨»Ùµ„E‘⁄BC±þ…œ£¨ ‘Àµ√˜DB°ÕBC£ª
”¶”√£∫
£®3£©»ÁÕº3£¨‘⁄Àƒ±þ–ŒABCD÷–£¨°œABC£Ω°œADC£Ω90°„£¨AB£ΩCB£¨°œBAD+°œBCD£Ω180°„£¨¡¨Ω”BD£¨BD£Ω7cm£¨«ÛÀƒ±þ–ŒABCDµƒ√ʪ˝£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨‘⁄Rt°˜ABC÷–£¨°œC=90°„£¨µ„D‘⁄BC…œ£¨µ„E‘⁄AB…œ£¨«“DE°ŒAC£¨AE=5£¨DE=2£¨DC=3£¨∂ص„P¥”µ„A≥ˆ∑¢£¨—ÿ±þAC“‘√ø√Î2∏ˆµ•Œª≥§µƒÀŸ∂»œÚ÷’µ„C‘À∂Ø£¨Õ¨ ±∂ص„F¥”µ„C≥ˆ∑¢£¨‘⁄œþ∂ŒCD…œ“‘√ø√Î1∏ˆµ•Œª≥§µƒÀŸ∂»œÚ÷’µ„D‘À∂Ø£¨…Ë‘À∂Ø ±º‰Œ™t√ΣÆ
£®1£©œþ∂ŒACµƒ≥§=________£ª
£®2£©µ±°˜PCF”ΰ˜EDFœýÀ∆ ±£¨«Ûtµƒ÷µ£Æ

≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨‘⁄∆Ω√Ê÷±Ω«◊¯±Íœµ÷–£¨°˜ABC»˝∏ˆ∂•µ„µƒ◊¯±Í∑÷±Œ™£∫A£®1£¨©Å4£©£¨B£®5£¨©Å4£©£¨C£®4£¨©Å1£©£Æ
£®1£©Ω´°˜ABCæ≠π˝∆Ω“∆µ√µΩ°˜A1B1C1£¨»Ùµ„Cµƒ”¶µ„C1µƒ◊¯±ÍŒ™£®2£¨5£©£¨‘Úµ„A£¨Bµƒ∂‘”¶µ„A1£¨B1µƒ◊¯±Í∑÷±Œ™°° °°£ª
£®2£©‘⁄»ÁÕºµƒ◊¯±Íœµ÷–ª≠≥ˆ°˜A1B1C1£¨≤¢ª≠≥ˆ”ΰ˜A1B1C1πÿ”⁄‘≠µ„O≥…÷––ƒ∂‘≥∆µƒ°˜A2B2C2£Æ

≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
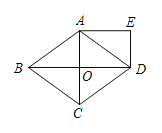
°æƒø°ø»ÁÕº£¨¡‚–ŒABCDµƒ∂‘Ω«œþAC£¨BDœýΩª”⁄µ„O£¨«“DE°ŒAC£¨AE°ŒBD£Æ
£®1£©«Û÷§£∫Àƒ±þ–ŒAODE «æÿ–Œ£Æ
£®2£©»ÙAB=5£¨BD=8£¨«Ûæÿ–ŒAODEµƒ÷Ð≥§£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
∞Ÿ∂»÷¬–≈ - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒÞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com