Question

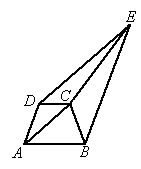
如图所示，在四边形ABCD中，AB∥CD，过B作BE∥AD，过D作DE∥AC交BE于E．求证．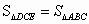

Answer 1

答案：略
解析：

证明：延长DC交BE于F，延长AC交BE于M． 则四边形ABFD和四边形AMED皆为平行四边形，且(同底等高)． 又∵(同底等高)， (同底等高)， ∴

提示：

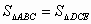计算面积，我们可以通过面积的计算公式，但是，对于一些特殊的图形可采取特殊的方法，如：同底同高的两个三角形面积相等，同底等高的三角形和平行四边形的面积比为1∶2，那么由给出条件中的几对平行线，可考虑构造几个平行四边形，延长DC交BE于F，延长AC交BE于M，则图中就有两个平行四边形，即平形四边形AMED和平形四边形ABFD，而且这两个平行四边形的底都为AD，且高都是平行线AD，BE之间的距离，即它们的高也相等，所以它们的面积相等，继续观察图形，可发现△ABC的面积恰好是平行四边形ABFD面积的一半，△DCE的面积恰好是平形四边形AMED面积的一半，因此可证明这两个三角形的面积相等．