
”¾ĢāÄæ”æČēĶ¼1£¬µćEŌŚ¾ŲŠĪABCDµÄ±ßADÉĻ£¬AD£½6£¬tan”ĻACD£½![]() £¬Į¬½ÓCE£¬Ļ߶ĪCEČʵćCŠż×Ŗ90”ć£¬µĆµ½Ļ߶ĪCF£¬ŅŌĻ߶ĪEFĪŖÖ±¾¶×ö”ŃO£®
£¬Į¬½ÓCE£¬Ļ߶ĪCEČʵćCŠż×Ŗ90”ć£¬µĆµ½Ļ߶ĪCF£¬ŅŌĻ߶ĪEFĪŖÖ±¾¶×ö”ŃO£®
£Ø1£©ĒėĖµĆ÷µćCŅ»¶ØŌŚ”ŃOÉĻµÄĄķÓÉ£»
£Ø2£©µćMŌŚ”ŃOÉĻ£¬ČēĶ¼2£¬MCĪŖ”ŃOµÄÖ±¾¶£¬ĒóÖ¤£ŗµćMµ½ADµÄ¾ąĄėµČÓŚĻ߶ĪDEµÄ³¤£»
£Ø3£©µ±”÷AEMĆ껿ȔµĆ×ī“óÖµŹ±£¬Ēó”ŃO°ė¾¶µÄ³¤£»
£Ø4£©µ±”ŃOÓė¾ŲŠĪABCDµÄ±ßĻąĒŠŹ±£¬¼ĘĖćÉČŠĪOCFµÄĆ껿£®
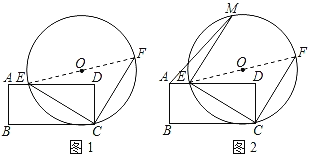
”¾“š°ø”æ£Ø1£©¼ū½āĪö£»£Ø2£©Ö¤Ć÷¼ū½āĪö£»£Ø3£©![]()
![]() £»£Ø4£©4¦Š£®
£»£Ø4£©4¦Š£®
”¾½āĪö”æ
£Ø1£©Į¬½ÓOC£¬ÓÉŠż×ŖµÄŠŌÖŹµĆ³ö”ĻECF£½90”ć£¬ÓÉÖ±½ĒČż½ĒŠĪŠ±±ßµÄÖŠĻߵĊŌÖŹµĆ³öOC£½OE£½OF£¬¼“æÉµĆ³öµćCŅ»¶ØŌŚ”ŃOÉĻ£»
£Ø2£©Ņ×Ö¤EM£½CE£¬¹żµćM×÷MN”ĶADÓŚN£¬ÓÉAASÖ¤µĆ”÷MEN”Õ”÷CED£¬µĆ³öMN£½DE£¬¼“æÉµĆ³ö½įĀŪ£»
£Ø3£©ÉčAE£½x£¬ŌņDE£½6©x£¬ÓÉ£Ø2£©µĆµćMµ½ADµÄ¾ąĄėµČÓŚĻ߶ĪDEµÄ³¤£¬ŌņS”÷AEM£½![]() ”Įx”Į£Ø6©x£©£½©
”Įx”Į£Ø6©x£©£½©![]() £Øx©3£©2+
£Øx©3£©2+![]() £¬µ±x£½3Ź±£¬”÷AEMĆ껿ȔµĆ×ī“óÖµ
£¬µ±x£½3Ź±£¬”÷AEMĆ껿ȔµĆ×ī“óÖµ![]() £¬“ĖŹ±£¬DE£½3£¬ÓÉtan”ĻACD£½
£¬“ĖŹ±£¬DE£½3£¬ÓÉtan”ĻACD£½![]() £½
£½![]() £¬µĆ³öCD£½4£¬Óɹ“¹É¶ØĄķµĆCE2£½DE2+CD2£¬Ēó³öCE£½5£¬Ņ×Ö¤”ĻCEF£½45”ć£¬ŌŚRt”÷CEFÖŠ£¬ÓÉEF£½
£¬µĆ³öCD£½4£¬Óɹ“¹É¶ØĄķµĆCE2£½DE2+CD2£¬Ēó³öCE£½5£¬Ņ×Ö¤”ĻCEF£½45”ć£¬ŌŚRt”÷CEFÖŠ£¬ÓÉEF£½![]() £¬¼“æÉµĆ³ö½į¹ū£»
£¬¼“æÉµĆ³ö½į¹ū£»
£Ø4£©µ±”ŃOÓė¾ŲŠĪABCDµÄ±ßĻąĒŠŹ±£¬Ö»ÓŠµćOÓėµćDÖŲŗĻŹ±“ęŌŚ£¬“ĖŹ±”ŃO°ė¾¶r£½CD£½4£¬”ĻCOF£½90”ć£¬ÓÉÉČŠĪĆ껿¹«Ź½¼“æÉµĆ³ö½į¹ū
£Ø1£©½ā£ŗµćCŅ»¶ØŌŚ”ŃOÉĻµÄĄķÓÉČēĻĀ£ŗ
Į¬½ÓOC£¬ČēĶ¼ĖłŹ¾£ŗ
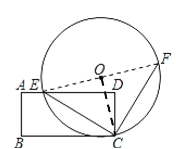
ÓÉŠż×ŖµÄŠŌÖŹµĆ£ŗ”ĻECF£½90”ć£¬
”ßEFŹĒ”ŃOµÄÖ±¾¶£¬OĪŖŌ²ŠÄ£¬
”ąOE£½OF£¬
”ąOC£½OE£½OF£¬
”ąµćCŅ»¶ØŌŚ”ŃOÉĻ£»
£Ø2£©Ö¤Ć÷£ŗÓÉŠż×ŖµÄŠŌÖŹµĆ£ŗ”ĻECF£½90”ć£¬CE£½CF£¬
”ßOE£½OF£¬
”ąCO”ĶEF£¬
”ßMCĪŖ”ŃOµÄÖ±¾¶£¬
”ąCM”ĶEF£¬OC£½OM£¬”ĻMEC£½90”ć£¬
”ąEM£½CE£¬
¹żµćM×÷MN”ĶADÓŚN£¬ČēĶ¼ĖłŹ¾£ŗ

”ß”ĻDEC+”ĻDCE£½90”ć£¬”ĻDEC+”ĻDEM£½90”ć£¬
”ą”ĻDEM£½”ĻDCE£¬
ŌŚ”÷MENŗĶ”÷CEDÖŠ£¬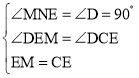 £¬
£¬
”ą”÷MEN”Õ”÷CED£ØAAS£©£¬
”ąMN£½DE£¬¼“µćMµ½ADµÄ¾ąĄėµČÓŚĻ߶ĪDEµÄ³¤£»
£Ø3£©½ā£ŗ”ßµćEŌŚ¾ŲŠĪABCDµÄ±ßADÉĻ£¬AD£½6£¬
”ą”ĻD£½90”ć£¬ÉčAE£½x£¬ŌņDE£½6©x£¬
ÓÉ£Ø2£©µĆ£ŗµćMµ½ADµÄ¾ąĄėµČÓŚĻ߶ĪDEµÄ³¤£¬
”ąS”÷AEM£½![]() ”Įx”Į£Ø6©x£©£½©
”Įx”Į£Ø6©x£©£½©![]() x2+3x£½©
x2+3x£½©![]() £Øx©3£©2+
£Øx©3£©2+![]() £¬
£¬
”ąµ±x£½3Ź±£¬”÷AEMĆ껿ȔµĆ×ī“óÖµ![]() £¬
£¬
“ĖŹ±£¬DE£½6©3£½3£¬
”ßtan”ĻACD£½![]() £½
£½![]() £¬
£¬
”ąCD£½![]() £½4£¬
£½4£¬
Óɹ“¹É¶ØĄķµĆ£ŗCE2£½DE2+CD2£¬¼“CE2£½32+42£¬
”ąCE£½5£¬
ÓÉ£Ø2£©µĆ£ŗCM”ĶEF£¬OC£½OM£¬”ĻMEC£½90”ć£¬
”ą”ĻCEF£½45”ć£¬
ŌŚRt”÷CEFÖŠ£¬EF£½![]() £½
£½![]() £½5
£½5![]() £¬
£¬
”ą”ŃO°ė¾¶µÄ³¤ĪŖ![]()
![]() £»
£»
£Ø4£©µ±”ŃOÓė¾ŲŠĪABCDµÄ±ßĻąĒŠŹ±£¬Ö»ÓŠµćOÓėµćDÖŲŗĻŹ±“ęŌŚ£¬“ĖŹ±”ŃO°ė¾¶r£½CD£½4£¬”ĻCOF£½90”ć£¬SÉČOCF=![]() £½4¦Š£®
£½4¦Š£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŌŚĘ½ĆęÖ±½Ē×ų±źĻµ![]() ÖŠ£ØČēĶ¼£©£¬ŅŃÖŖ¶ž“ĪŗÆŹż
ÖŠ£ØČēĶ¼£©£¬ŅŃÖŖ¶ž“ĪŗÆŹż![]() £ØĘäÖŠa”¢b”¢cŹĒ³£Źż£¬ĒŅa”Ł0£©µÄĶ¼Ļń¾¹żµćA£Ø0£¬-3£©”¢B£Ø1£¬0£©”¢C£Ø3£¬0£©£¬ĮŖ½įAB”¢AC£®
£ØĘäÖŠa”¢b”¢cŹĒ³£Źż£¬ĒŅa”Ł0£©µÄĶ¼Ļń¾¹żµćA£Ø0£¬-3£©”¢B£Ø1£¬0£©”¢C£Ø3£¬0£©£¬ĮŖ½įAB”¢AC£®
£Ø1£©ĒóÕāøö¶ž“ĪŗÆŹżµÄ½āĪöŹ½£»
£Ø2£©µćDŹĒĻ߶ĪACÉĻµÄŅ»µć£¬ĮŖ½įBD£¬Čē¹ū![]() £¬Ēótan”ĻDBCµÄÖµ£»
£¬Ēótan”ĻDBCµÄÖµ£»
£Ø3£©Čē¹ūµćEŌŚøƶž“ĪŗÆŹżĶ¼ĻńµÄ¶Ō³ĘÖįÉĻ£¬µ±ACĘ½·Ö”ĻBAEŹ±£¬ĒóµćEµÄ×ų±ź£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
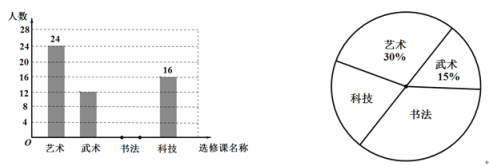
”¾ĢāÄæ”æÄ³ÖŠŃ§½ųŠŠ»łÓŚŃ§ÉśŗĖŠÄĖŲŃųæĪ³ĢĢåĻµµÄæŖ·¢£¬Ń§Š£¼Ę»®æŖÉč£ŗŅÕŹõ”¢ĪäŹõ”¢Źé·Ø”¢æĘ¼¼¹²ĖÄĆÅŃ”ŠŽæĪ£¬²¢æŖÕ¹ĮĖŅŌ”°Äć×īĻė²Ī¼ÓµÄŃ”ŠŽæĪŹĒÄÄĆÅ?£Ø±ŲŃ”ĒŅֻєŅ»ĆÅŃ”ŠŽæĪ£©”±ĪŖÖ÷ĢāµÄµ÷²é»ī¶Æ£¬ŌŚČ«Š£·¶Ī§ÄŚĖ껜³éČ”²æ·Öѧɜ½ųŠŠĪŹ¾ķµ÷²é£¬½«µ÷²é½į¹ūÕūĄķŗó»ęÖĘ³ÉČēĶ¼ĖłŹ¾µÄ²»ĶźÕūµÄĶ³¼ĘĶ¼.ĒėÄćøł¾ŻĶ³¼ĘĶ¼µÄŠÅĻ¢»Ų“šĻĀĮŠĪŹĢā£ŗ
(1)±¾“Īµ÷²é¹²³éČ”ĮĖ¶ąÉŁĆūѧɜ?
(2)·Ö±šĒó³ö²Ī¼Óµ÷²éµÄѧɜ֊єŌńĪäŹõŗĶŹé·ØŃ”ŠŽæĪµÄČĖŹż£¬²¢²¹Č«ĢõŠĪĶ³¼ĘĶ¼£»
(3)ČōøĆ֊ѧ¹²ÓŠ 1600 Ćūѧɜ£¬ĒėÄć¹Ą¼ĘøĆ֊ѧєŌńæĘ¼¼Ń”ŠŽæĪµÄѧɜ“óŌ¼ÓŠ¶ąÉŁĆū£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖ£ŗRt”÷ABC£¬”ĻC£½90”ć£®
£Ø1£©µćEŌŚBC±ßÉĻ£¬ĒŅ”÷ACEµÄÖܳ¤ĪŖAC£«BC£¬ŅŌĻ߶ĪAEÉĻŅ»µćOĪŖŌ²ŠÄµÄ”ŃOĒ”ÓėAB”¢BC±ß¶¼ĻąĒŠ£®ĒėÓĆĪŽæĢ¶ČµÄÖ±³ßŗĶŌ²¹ęČ·¶ØµćE”¢OµÄĪ»ÖĆ£»
£Ø2£©ČōBC£½8£¬AC£½4£¬Ēó”ŃOµÄ°ė¾¶£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŌŚŅ»øö²»ĶøĆ÷µÄæŚ“üÖŠ·ÅČė![]() øö“󊔊Īד¼øŗõĶźČ«ĻąĶ¬ŹµŃéÓĆµÄ¼¦µ°£¬¼¦µ°µÄÖŹĮæÓŠĪ¢Š”µÄ²ī¾ą£ØÓĆŹÖøŠ¾õ²»µ½²īŅģ£©£¬ÖŹĮæ·Ö±šĪŖ
øö“󊔊Īד¼øŗõĶźČ«ĻąĶ¬ŹµŃéÓĆµÄ¼¦µ°£¬¼¦µ°µÄÖŹĮæÓŠĪ¢Š”µÄ²ī¾ą£ØÓĆŹÖøŠ¾õ²»µ½²īŅģ£©£¬ÖŹĮæ·Ö±šĪŖ![]() ”¢
Ӣ![]() Ӣ
”¢![]() æĖ£¬ŅŃÖŖĖ껜µÄĆž³öŅ»øö¼¦µ°£¬Ćžµ½
æĖ£¬ŅŃÖŖĖ껜µÄĆž³öŅ»øö¼¦µ°£¬Ćžµ½![]() æĖŗĶ
æĖŗĶ![]() æĖµÄ¼¦µ°µÄøÅĀŹŹĒĻąµČµÄ£®
æĖµÄ¼¦µ°µÄøÅĀŹŹĒĻąµČµÄ£®
£Ø1£©ĒóÕāĖÄøö¼¦µ°ÖŹĮæµÄÖŚŹżŗĶÖŠĪ»Źż
£Ø2£©Š”Ć÷×öŹµŃéŠčŅŖÄĆ×ßŅ»øö¼¦µ°£¬·¼·¼ŌŚŠ”Ć÷ÄĆ×ßŗó“ÓŹ£ĻĀµÄČżøö¼¦µ°ÖŠĖ껜µÄÄĆ×ßŅ»øö
¢ŁĶعż¼ĘĖć·ÖĪöŠ”Ć÷ÄĆ×ßŅ»øö¼¦µ°ŗó£¬Ź£ĻĀµÄČżøö¼¦µ°ÖŹĮæµÄÖŠĪ»ŹżŹĒ¶ąÉŁ£æ
¢Ś¼ŁÉ芔Ć÷ÄĆ×ߵļ¦µ°ÖŹĮæĪŖ![]() æĖ£¬·¼·¼Ė껜µÄÄĆ³öŅ»øö¼¦µ°ŗóÓÖ·Å»Ų£¬Ö®ŗóŌŁĖ껜µÄÄĆ³öŅ»øö¼¦µ°£¬ĒėÓĆŹ÷דĶ¼Ēó·¼·¼Į½“ĪÄƵ½¶¼ŹĒ
æĖ£¬·¼·¼Ė껜µÄÄĆ³öŅ»øö¼¦µ°ŗóÓÖ·Å»Ų£¬Ö®ŗóŌŁĖ껜µÄÄĆ³öŅ»øö¼¦µ°£¬ĒėÓĆŹ÷דĶ¼Ēó·¼·¼Į½“ĪÄƵ½¶¼ŹĒ![]() æĖµÄ¼¦µ°µÄøÅĀŹ£æ
æĖµÄ¼¦µ°µÄøÅĀŹ£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµ![]() ÖŠ£¬ŗÆŹż
ÖŠ£¬ŗÆŹż![]() µÄĶ¼Ļó
µÄĶ¼Ļó![]() ¾¹żµć
¾¹żµć![]() £¬Ö±Ļß
£¬Ö±Ļß![]() Óė
Óė![]() Öį½»ÓŚµć
Öį½»ÓŚµć![]() £®
£®
£Ø1£©Ēó![]() µÄÖµ¼°µć
µÄÖµ¼°µć![]() µÄ×ų±ź£»
µÄ×ų±ź£»
£Ø2£©Ö±Ļß![]() ÓėŗÆŹż
ÓėŗÆŹż![]() µÄĶ¼Ļó
µÄĶ¼Ļó![]() ½»ÓŚµć
½»ÓŚµć![]() £¬¼ĒĶ¼Ļó
£¬¼ĒĶ¼Ļó![]() ŌŚµć
ŌŚµć![]() £¬
£¬![]() Ö®¼äµÄ²æ·ÖÓėĻ߶Ī
Ö®¼äµÄ²æ·ÖÓėĻ߶Ī![]() £¬
£¬![]() £¬
£¬![]() Ī§³ÉµÄĒųÓņ£Ø²»ŗ¬±ß½ē£©ĪŖ
Ī§³ÉµÄĒųÓņ£Ø²»ŗ¬±ß½ē£©ĪŖ![]() £®
£®
¢Łµ±![]() Ź±£¬Ö±½ÓŠ“³öĒųÓņ
Ź±£¬Ö±½ÓŠ“³öĒųÓņ![]() ÄŚµÄÕūµćøöŹż£»
ÄŚµÄÕūµćøöŹż£»
¢ŚČōĒųÓņ![]() ÄŚĒ”ÓŠ2øöÕūµć£¬½įŗĻŗÆŹżĶ¼Ļó£¬Ēó
ÄŚĒ”ÓŠ2øöÕūµć£¬½įŗĻŗÆŹżĶ¼Ļó£¬Ēó![]() µÄȔֵ·¶Ī§£®
µÄȔֵ·¶Ī§£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
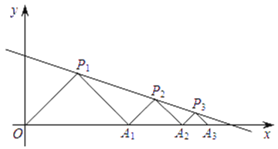
”¾ĢāÄæ”æČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬![]() £¬
£¬![]() £¬
£¬![]() £¬£®£®£®¶¼ŹĒµČŃüÖ±½ĒČż½ĒŠĪ£¬ĘäÖ±½Ē¶„µć
£¬£®£®£®¶¼ŹĒµČŃüÖ±½ĒČż½ĒŠĪ£¬ĘäÖ±½Ē¶„µć![]() £¬
£¬![]() £¬
£¬![]() £¬£®£®£®¾łŌŚÖ±Ļß
£¬£®£®£®¾łŌŚÖ±Ļß![]() ÉĻ£¬Éč
ÉĻ£¬Éč![]() £¬
£¬![]() £¬
£¬![]() £¬£®£®£®µÄĆ껿·Ö±šĪŖ
£¬£®£®£®µÄĆ껿·Ö±šĪŖ![]() £¬
£¬![]() £¬
£¬![]() £¬£®£®£®£¬ŅĄ¾ŻĶ¼ŠĪĖł·“Ó³µÄ¹ęĀÉ£¬S2020£½__________£®
£¬£®£®£®£¬ŅĄ¾ŻĶ¼ŠĪĖł·“Ó³µÄ¹ęĀÉ£¬S2020£½__________£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
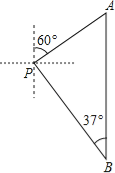
”¾ĢāÄæ”抔ĮĮŅ»¼ŅŌŚŅ»ŗž²“ÖŠÓĪĶę£¬ŗž²“ÖŠÓŠŅ»¹Āµŗ£¬ĀčĀčŌŚ¹ĀµŗP“¦¹Ūæ“Š”ĮĮÓė°Ö°ÖŌŚŗžÖŠ»®“¬£ØČēĶ¼ĖłŹ¾£©£®Š”“¬“ÓP“¦³ö·¢£¬ŃŲ±±Ę«¶«60”ć·½Ļņ»®ŠŠ200Ć×µ½A“¦£¬½Ó×ÅĻņÕżÄĻ·½Ļņ»®ŠŠŅ»¶ĪŹ±¼äµ½B“¦£®ŌŚB“¦Š”ĮĮ¹Ū²āµ½ĀčĀčĖłŌŚµÄP“¦ŌŚ±±Ę«Ī÷37”ćµÄ·½ĻņÉĻ£¬ÕāŹ±Š”ĮĮÓėĀčĀčĻą¾ą¶ąÉŁĆףؾ«Č·µ½1Ć×£©£æ
£Ø²Īæ¼Źż¾Ż£ŗsin37”ć”Ö0.60£¬cos37”ć”Ö0.80£¬tan37”ć”Ö0.75£¬![]() ”Ö1.41£¬
”Ö1.41£¬![]() ”Ö1.73£©
”Ö1.73£©
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬Å×ĪļĻß![]() Óė
Óė![]() Öį½»ÓŚA£¬BĮ½µć£ØµćAŌŚµćBµÄ×ó²ą£©£¬Ö±Ļß
Öį½»ÓŚA£¬BĮ½µć£ØµćAŌŚµćBµÄ×ó²ą£©£¬Ö±Ļß![]() ÓėÅ×ĪļĻß½»ÓŚ
ÓėÅ×ĪļĻß½»ÓŚ![]() Į½µć£¬ĘäÖŠµć
Į½µć£¬ĘäÖŠµć![]() µÄŗį×ų±źĪŖ2£®
µÄŗį×ų±źĪŖ2£®
£Ø1£©ĒóA£¬BĮ½µćµÄ×ų±ź¼°Ö±ĻßACµÄ±ķ“ļŹ½£»
£Ø2£©PŹĒĻ߶ĪACÉĻŅ»¶Æµć£ØPÓėA£¬C²»ÖŲŗĻ£©£¬¹żµćP×÷![]() ÖįµÄĘ½ŠŠĻß½»Å×ĪļĻßÓŚµćE£¬Ēó
ÖįµÄĘ½ŠŠĻß½»Å×ĪļĻßÓŚµćE£¬Ēó![]() Ć껿µÄ×ī“óÖµ£»
Ć껿µÄ×ī“óÖµ£»
£Ø3£©µćHŹĒÅ×ĪļĻßÉĻŅ»¶Æµć£¬ŌŚ![]() ÖįÉĻŹĒ·ń“ęŌŚµćF£¬Ź¹µĆ
ÖįÉĻŹĒ·ń“ęŌŚµćF£¬Ź¹µĆ![]() ĖÄøöµćĪŖ¶„µćµÄĖıߊĪŹĒĘ½ŠŠĖıߊĪ£æČē¹ū“ęŌŚĒėÖ±½ÓŠ“³öĖłÓŠĀś×ćĢõ¼žµÄµćF×ų±ź£»Čē¹ū²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£®
ĖÄøöµćĪŖ¶„µćµÄĖıߊĪŹĒĘ½ŠŠĖıߊĪ£æČē¹ū“ęŌŚĒėÖ±½ÓŠ“³öĖłÓŠĀś×ćĢõ¼žµÄµćF×ų±ź£»Čē¹ū²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£®

²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com